Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: \(P\left(x\right)=3x^2-x-1\)
\(Q\left(x\right)=-3x^2-4x-2\)
b: \(G\left(x\right)=3x^2-x-1+3x^2+4x+2=6x^2+3x+1\)
c: Để G(x)-6x-1=0 thì 6x2-3x=0
=>3x(2x-1)=0
=>x=0 hoặc x=1/2

`@` `\text {Ans}`
`\downarrow`
`a)`
`P(x) =`\(3x^2+7+2x^4-3x^2-4-5x+2x^3\)
`= (3x^2 - 3x^2) + 2x^4 + 2x^3 - 5x + (7-4)`
`= 2x^4 + 2x^3 - 5x + 3`
`Q(x) =`\(3x^3+2x^2-x^4+x+x^3+4x-2+5x^4\)
`= (5x^4 - x^4) + (3x^3 + x^3) + 2x^2 + (x + 4x)- 2`
`= 4x^4 + 4x^3 + 2x^2 + 5x - 2`
`b)`
`P(-1) = 2*(-1)^4 + 2*(-1)^3 - 5*(-1) + 3`
`= 2*1 + 2*(-1) + 5 + 3`
`= 2 - 2 + 5 + 3`
`= 8`
___
`Q(0) = 4*0^4 + 4*0^3 + 2*0^2 + 5*0 - 2`
`= 4*0 + 4*0 + 2*0 + 5*0 - 2`
`= -2`
`c)`
`G(x) = P(x) + Q(x)`
`=> G(x) = 2x^4 + 2x^3 - 5x + 3 + 4x^4 + 4x^3 + 2x^2 + 5x - 2`
`= (2x^4 + 4x^4) + (2x^3 + 4x^3) + 2x^2 + (-5x + 5x) + (3 - 2)`
`= 6x^4 + 6x^3 + 2x^2 + 1`
`d)`
`G(x) = 6x^4 + 6x^3 + 2x^2 + 1`
Vì `x^4 \ge 0 AA x`
`x^2 \ge 0 AA x`
`=> 6x^4 + 2x^2 \ge 0 AA x`
`=> 6x^4 + 6x^3 + 2x^2 + 1 \ge 0`
`=> G(x)` luôn dương `AA` `x`

a) Bậc P(x) = 4 + 3 + 1 = 8
Bậc của Q (x) = 2 + 3 + 1 = 6
b) P(x) + Q ( x) = x4 + x3 -2x + 1 + 2x2 -2x3 + x- 5
= x4 -x3 + 2x2 -x - 4
P(x) - Q (x) = x4 +x3 -2x + 1 - 2x2 -2x3 + x - 5
= x4 + 3x 3 -2x2 - 3x + 6
a) Bậc của đa thức P(x) là: 4+3+1=8
Bậc xủa đa thức Q(x) là: 2+3+1=6
b) P(x)+Q(x)=(x4+x3-2x+1)+(2x2-2x3+x-5)
P(x)+Q(x)=x4+x3-2x+1+2x2-2x3+x-5
P(x)+Q(x)=x4-x3+2x2-x-4
P(x)-Q(x)=(x4+x3-2x+1)-(2x2-2x3+x-5)
P(x)-Q(x)=x4+x3-2x+1-2x2+2x3-x+5
P(x)-Q(x)=x4+3x3-2x2-3x+6

a, \(P\left(x\right)=4x^3+2x-3+2x-2x^2-1\\ =4x^3-2x^2+\left(2x+2x\right)+\left(-3-1\right)\\ =4x^3-2x^2+4x-4\)
Bậc của P(x) là 3
\(Q\left(x\right)=6x^3-3x+5-2x+3x^2\\ =6x^3+3x^2+\left(-3x-2x\right)+5\\ =6x^3+3x^2-5x+5\)
Bậc của Q(x) là 3
b, \(M\left(x\right)=P\left(x\right)+Q\left(x\right)=4x^3-2x^2+4x-4+6x^3+3x^2-5x+5\\ =\left(4x^3+6x^3\right)+\left(-2x^2+3x^2\right)+\left(4x-5x\right)+\left(-4+5\right)\\ =10x^3+x^2-x+1\)

mình khuyên bạn nên đưa lên từng câu một thôi chứ bạn đưa lên dài thế này ai nhìn cũng khong muốn làm đâu nha
BẠN HÃY DÙNG Fx ĐỂ GHI CHO DỄ HIỂU NHÉ BẠN

\(P\left(x\right)+Q\left(x\right)=\left(2x^4+x^3-4x+5\right)+\left(x^4+3x^3+2x-1\right)\)
\(=2x^4+x^3-4x+5+x^4+3x^3+2x-1\)
\(=\left(2x^4+x^4\right)+\left(x^3+3x^3\right)+\left(-4x+2x\right)+\left(5-1\right)\)
\(=3x^4+4x^3-2x+4\)
\(R\left(x\right)+P\left(x\right)=x^4-2x^2+1\)
\(\Rightarrow R\left(x\right)=\left(x^4-2x^2+1\right)-P\left(x\right)\)
\(\Rightarrow R\left(x\right)=\left(x^4-2x^2+1\right)-\left(2x^4+x^3-4x+5\right)\)
\(\Rightarrow R\left(x\right)=x^4-2x^2+1-2x^4-x^3+4x-5\)
\(\Rightarrow R\left(x\right)=\left(x^4-2x^4\right)+\left(-2x^2\right)+\left(1-5\right)+\left(-x^3\right)+4x\)
\(\Rightarrow R\left(x\right)=-x^4-2x^2-4-x^3+4x\)

` P(x) = x^3-2x^2+x-2`
`Q(x) = 2x^3 - 4x^2+ 3x – 56`
a) `P(x) -Q(x)`
`= x^3-2x^2+x-2 - 2x^3 +4x^2 -3x +56`
`=(x^3-2x^3) +(4x^2-2x^2) +(x-3x) +(-2+56)`
`= -x^2 +2x^2 -2x +54`
b) Thay `x=2` vào `P(x)` ta đc
`P(2) = 2^3 -2*2^2 +2-2`
`= 8-8+2-2 =0`
Vậy chứng tỏ `x=2` là nghiệm của đa thức `P(x)`
Thay `x=2` vào `Q(x)` ta đc
`Q(2) = 2*2^3 -4*2^2 +3*2-56`
`=16 -16+6-56`
`= -50`
Vậy chứng tỏ `x=2` là ko nghiệm của đa thức `Q(x)`

a) \(P_{\left(x\right)}=3x^2+2x^3+2x+5-x^2-x-5\)
\(P_{\left(x\right)}=2x^3+2x^2+x\)
\(Q_{\left(x\right)}=x^3-2x-2+3x-x^2+1\)
\(Q_{\left(x\right)}=x^3-x^2+x-1\)
b) ta có: \(P_{\left(x\right)}+Q_{\left(x\right)}=\left(2x^3+2x^2+x\right)+\left(x^3-x^2+x-1\right)\)
\(=\left(2x^3+x^3\right)+\left(2x^2-x^2\right)+\left(x+x\right)-1\)
\(=3x^3+x^2+2x-1\)
ta có: \(P_{\left(x\right)}-Q_{\left(x\right)}=\left(2x^3+2x^2+x\right)-\left(x^3-x^2+x-1\right)\)
\(=\left(2x^3-x^3\right)+\left(2x^2+x^2\right)+\left(x-x\right)+1\)
\(=x^3+3x^2+1\)
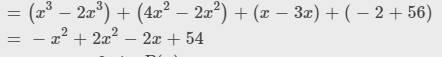
chiều học rồi