Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)
Do A và B đều là kim loại hóa trị II nên ta sử dụng phương pháp trung bình coi A và B là một chất gọi là X
=> CT chung của 2 muối là XCO3
Ta có nCO2 = \(\dfrac{1,12}{22,4}\) = 0,05 ( mol )
XCO3 + H2SO4 → XSO4 + H2O + CO2
0,05 <---- 0,05 <---0,05 <-- 0,05 < -0,05
bảo toàn khối lượng ta có
mXSO4 = mXCO3 + mH2SO4 - mH2O - mCO2
= 4,68 + ( 98 . 0,05 ) - ( 18 . 0,05 ) - ( 44 . 0,05 )
= 6,48 ( gam )
b) MXCO3 = mXCO3 : nXCO3 = 4,68 : 0,05 = 93,6
=> X = 93,6 - 12 - 16 . 3 = 33,6
có nACO3 : nBCO3 = 2 : 3
và nACO3 + nBCO3 = 0,05
=> nACO3 = 0,02 và nBCO3 = 0,03
=> nA = 0,02 và nB = 0,03
=> ( 0,02 . A + 5 : 3 . 0,03 . B) / 0,05 = 33,6
=> A = 24 ( là magie - Mg ) do B = A . 5 :3
=> B = 40 ( là canxi - Ca )
=> mMgCO3 = 1,68 ( gam )
=> %mMgCO3 = \(\dfrac{1,68}{4,68}\) . 100 \(\approx\) 36 %
=> %mCaCO3 = 100 - 36 = 64%

Áp dụng phương pháp tăng giảm khối lượng
X CO 3 + 2HCl → X Cl 2 + CO 2 + H 2 O
Y 2 CO 3 3 + 6HCl → 2Y Cl 3 + H 2 O + CO 2
0,03 mol CO 2 bay ra thì khối lượng tăng : 0,03 x 11 gam
Tổng khối lượng muối clorua tạo thành : 10 + (0,03 x 11)= 10,33 (gam)
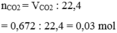
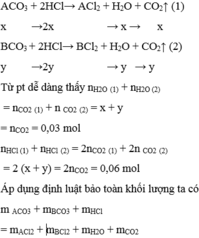
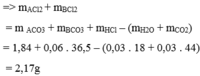

\(n_{CO_2}=\dfrac{0.672}{22.4}=0.03\left(mol\right)\)
\(ACO_3+2HCl\rightarrow ACl_2+CO_2+H_2O\)
Ta có :
\(n_{HCl}=2\cdot0.03=0.06\left(mol\right)\)
\(n_{H_2O}=0.03\left(mol\right)\)
Bảo toàn khối lượng :
\(m_{Muối}=1.84+0.06\cdot36.5-0.03\cdot44-0.03\cdot18=2.17\left(g\right)\)
ACO3 +2 HCl -> ACl2 + CO2 + H2O
Ta có: \(n_{ACO_3}=n_{CO_2}=0,03\left(mol\right)\\ \Rightarrow m_{muối}=m_{ACO_3}+\left(71-60\right).0,03=2,17\left(g\right)\)
=> CHỌN B