Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đặt: \(\left\{{}\begin{matrix}n_{Fe}=x\left(mol\right)\\n_{Cu}=y\left(mol\right)\end{matrix}\right.\) (x,y: nguyên, dương)
PTHH: Fe + 4 HNO3 -> Fe(NO3)3 + NO + 2 H2O
x_____________________________x(mol)
3 Cu + 8 HNO3 ->3 Cu(NO3)2 + 2 NO + 4 H2O
y_________________________2/3y(mol)
Ta có hpt: \(\left\{{}\begin{matrix}56x+64y=12,4\\x+\dfrac{2}{3}y=0,15\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0,05\\y=0,15\end{matrix}\right.\)
=>mFe=0,05.56=2,8(g)
=>%mFe=(2,8/12,4).100=22,581%
=>%mCu= 77,419%

\(Đặt:\left\{{}\begin{matrix}n_{Fe}=x\left(mol\right)\\n_{Cu}=y\left(mol\right)\end{matrix}\right.\\ Fe\rightarrow Fe^{3+}+3e\\ Cu\rightarrow Cu^{2+}+2e\\ 4H^++NO_3^-+3e\rightarrow NO+2H_2O\\ Bảotoàne:3x+2y=0,4.3\\ Tacó:56x+64y=30,4\\ \Rightarrow\left\{{}\begin{matrix}x=0,2\\y=0,3\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}\%m_{Fe}=36,84\%\\\%m_{Cu}=63,16\%\end{matrix}\right.\\ n_{HNO_3}=4n_{NO}=0,4.4=1,6\left(mol\right)\\ \Rightarrow V_{HNO_3}=\dfrac{1,6}{1}=1,6\left(l\right)\\ m_{muối}=m_{Fe\left(NO_3\right)_3}+m_{Cu\left(NO_3\right)_2}=0,2.242+0,3.188=104,8\left(g\right)\)

- Viết đúng ptpư:
\(Fe+4HNO_3\rightarrow Fe\left(NO_3\right)_3+NO+2H_2O\)
\(3Cu+8HNO_3\rightarrow2Cu\left(NO_3\right)_2+2NO+4H_2O\)
\(nNO=0,04\left(mol\right)\)
Gọi nFe là x(mol) ; nCu là y(mol)
ta có hệ pt:
\(\left\{{}\begin{matrix}m_{hh}=56x+64y=3,04\\nNO=x+\dfrac{2}{3y}=0,04\end{matrix}\right.\)
Giải hệ ta được: x = 0,02 mol ; y = 0,03 mol
\(\Rightarrow mFe=0,02.56=1,12\left(g\right)\)
\(mCu=0,03.64=1,92\left(g\right)\)

Gọi nAl = x (mol), nCu = y (mol); nNO2 = 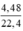 = 0,2 mol
= 0,2 mol
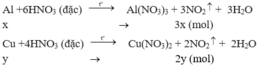
Theo pt: nNO2(1) = 3. nAl = 3.x mol
nNO2(2) = 2. nCu = 2y mol
⇒ Tổng nNO2 = 3x + 2y = 0,2 mol
Ta có hệ phương trình
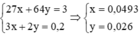
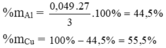

Gọi $n_{Cu} = a(mol) ; n_{Al} = b(mol) \Rightarrow 64a + 27b = 3(1)$
$Cu^0 \to Cu^{+2} + 2e$
$Al^0 \to Al^{+3} + 3e$
$N^{+5} + 1e \to N^{+4}$
Bảo toàn electron :
$2a + 3b = 0,2(2)$
Từ (1)(2) suy ra $a = \dfrac{3}{115} ; b = \dfrac{17}{345}$
\(\%m_{Cu}=\dfrac{\dfrac{3}{115}.64}{3}.100\%=55,65\%\\ \%m_{Al}=100\%-55,65\%=44,35\%\)
Gọi số mol của Cu và Al lần lượt là x,y (mol) (x,y>0)
\(Cu+4HNO_{3\left(đ\right)}\underrightarrow{to}Cu\left(NO_3\right)_2+2NO_2+2H_2O\\ x..................................2x\left(mol\right)\\ Al+6HNO_{3\left(đ\right)}\underrightarrow{to}Al\left(NO_3\right)_3+3NO_2+3H_2O\\ y...............................3y\left(mol\right)\)
\(\left\{{}\begin{matrix}64x+27y=3\\2x+3y=0,2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{3}{115}\\y=\dfrac{17}{345}\end{matrix}\right.\)
\(\left\{{}\begin{matrix}\%m_{Cu}=\dfrac{\dfrac{3}{115}.64}{3}.100\approx55,652\%\\\%m_{Al}\approx44,348\%\end{matrix}\right.\\ \)
