Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đường tròn tâm O là hình có tâm đối xứng. Tâm đối xứng của (O) là tâm của đường tròn đó.

Khi quay tấm bìa, các kết quả có thể xảy ra là:
Mũi tên chỉ vào ô số 1; Mũi tên chỉ vào ô số 2; Mũi tên chỉ vào ô số 3; Mũi tên chỉ vào ô số 4; Mũi tên chỉ vào ô số 5; Mũi tên chỉ vào ô số 6; Mũi tên chỉ vào ô số 7; Mũi tên chỉ vào ô số 8.
- Các kết quả thuận lợi cho biến cố \(A\) mũi tên chỉ vào ô số chẵn là ô số 2; ô số 4; ô số 6; ô số 8.
- Các kết quả thuận lợi cho biến cố \(B\)mũi tên chỉ vào ô số chia hết cho 4 là ô số 4; ô số 8.
- Các kết quả thuận lợi cho biến cố \(C\) mũi tên chỉ vào ô số nhỏ hơn 3 là ô số 1; ô số 2.

Với \(n=4\), ta chỉ ra một trường hợp sau thỏa mãn:
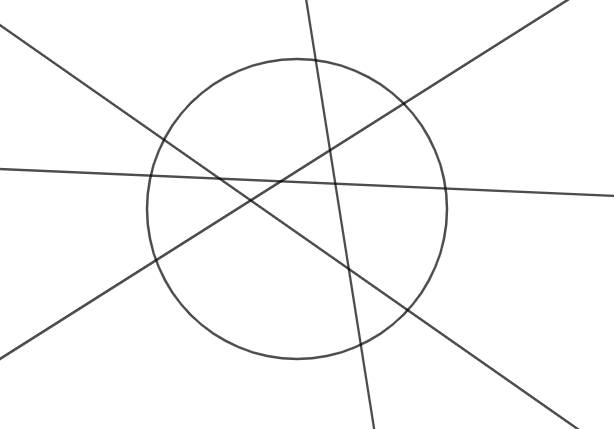
Với \(n\le3\), ta xét trường hợp mà n đường thẳng chia hình tròn thành nhiều miền nhất. (Tức là không có 3 đường nào đồng quy và không có 2 đường thẳng nào song song hoặc cắt nhau bên ngoài hình tròn). Khi đó đường tròn bị chia thành tối đa 7 miền, không thỏa mãn.
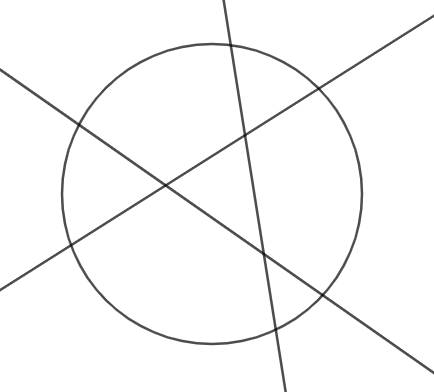
Vậy \(min_n=4\)

Ta chia hình vuông đề cho thành 16 hình vuông nhỏ bằng nhau (như hình vẽ)

Ta được độ dài cạnh của hình vuông nhỏ là 1
Có 33 điểm đặt vào 16 hình vuông theo nguyên lí Dirichlet
Suy ra tồn tại một hình vuông nhỏ chứa ít nhất 3 điểm
Giả sử hình vuông nhỏ đó là: ABCD (AC cắt BD tại O)
Có \(OA=\frac{AC}{2}=\frac{\sqrt{AB^2+BC^2}}{2}=\frac{\sqrt{1^2+1^2}}{2}=\frac{\sqrt{2}}{2}\)\(\Rightarrow AC=BD=\sqrt{2}\)
Giả sử 3 điểm đó trùng với 3 trong 4 đỉnh bất kì của hình vuông ABCD thì phần chung của ba hình tròn chứa toàn bộ hình vuông và như vậy đã tồn tại 3 điểm thỏa mãn yêu cầu bài toán.
Nếu trong 3 điểm có điểm nằm bên trong hình vuông thì phần chung của ba hình tròn cũng chứa toàn bộ hình vuông và như vậy đã tồn tại 3 điểm thỏa mãn yêu cầu bài toán
KL: tồn tại 3 điểm trong các điểm đã cho thỏa mãn yêu cầu bài toán.

A B C D E M h N
Kéo dài AB về phía B một đoạn BE=DC. Nối DE cắt BC tại M.
Do CD // BE nên ta có tam giác MDC = tam giác MEB (trường hợp g.c.g). Suy ra dt(ABCD)=dt(ABMD) + dt(MDC) = dt(ABMD) + dt(MEB) = dt(DAE) = 1/2 .AE . h =1/2 (AB + BE).h = \(\dfrac{AB+CD}{2}.h\)
b) Theo câu a) thì diện tích hình thang ABCD bằng diện tích tam giác DAE nên ta nối D với trung điểm N của AE thì DN sẽ chia tam giác DAE thành 2 phần bằng nhau. Khi đó diện tích tam giác DAN bằng nửa diện tích hình thang ABCD.



thầy đã trả lời, bn hãy tự vẽ lại nha!