Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C.
Đặt u = G ( x ) d v = f ( x ) d x ⇒ d u = G ( x ) ' d x = g ( x ) d x v = ∫ f ( x ) d x = F ( x )
Suy ra: I = G ( x ) F ( x ) 2 0 - ∫ 0 2 F ( x ) g ( x ) d x
= G(2)F(2) – G(0)F(0) – 3 = 1 – 0 – 3 = -2.

\(f'\left(x\right)=\left(x-1\right)\left(x+1\right)\left(x+1\right)\left(x-2\right)=\left(x+1\right)^2\left(x-1\right)\left(x-2\right)\)
\(f'\left(x\right)=0\Rightarrow\left[{}\begin{matrix}x=1\\x=2\end{matrix}\right.\) (chỉ quan tâm nghiệm bội lẻ)
\(g'\left(x\right)=\left(1-2x\right)f'\left(x-x^2\right)=0\Rightarrow\left[{}\begin{matrix}x=\dfrac{1}{2}\\f'\left(x-x^2\right)=0\end{matrix}\right.\)
\(f'\left(x-x^2\right)=0\Rightarrow\left[{}\begin{matrix}x-x^2=1\\x-x^2=2\end{matrix}\right.\) (đều vô nghiệm)
\(\Rightarrow g\left(x\right)\) đồng biến khi \(x< \dfrac{1}{2}\) và nghịch biến khi \(x>\dfrac{1}{2}\)
\(\Rightarrow C\) đúng (do \(\left(-\infty;-1\right)\subset\left(-\infty;\dfrac{1}{2}\right)\)

d: ĐKXĐ: \(x^2-1< >0\)
=>\(x^2\ne1\)
=>\(x\notin\left\{1;-1\right\}\)
Vậy: TXĐ là D=R\{1;-1}
b: ĐKXĐ: \(2-x^2>0\)
=>\(x^2< 2\)
=>\(-\sqrt{2}< x< \sqrt{2}\)
Vậy: TXĐ là \(D=\left(-\sqrt{2};\sqrt{2}\right)\)
a: ĐKXĐ: \(x-1>0\)
=>x>1
Vậy: TXĐ là \(D=\left(1;+\infty\right)\)
c: ĐKXĐ: \(x^2+x-6>0\)
=>\(x^2+3x-2x-6>0\)
=>\(\left(x+3\right)\left(x-2\right)>0\)
TH1: \(\left\{{}\begin{matrix}x+3>0\\x-2>0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>2\\x>-3\end{matrix}\right.\)
=>x>2
TH2: \(\left\{{}\begin{matrix}x+3< 0\\x-2< 0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x< -3\\x< 2\end{matrix}\right.\)
=>x<-3
Vậy: TXĐ là \(D=\left(2;+\infty\right)\cup\left(-\infty;-3\right)\)
e: ĐKXĐ: \(x^2-2>0\)
=>\(x^2>2\)
=>\(\left[{}\begin{matrix}x>\sqrt{2}\\x< -\sqrt{2}\end{matrix}\right.\)
Vậy: TXĐ là \(D=\left(-\infty;-\sqrt{2}\right)\cup\left(\sqrt{2};+\infty\right)\)
f: ĐKXĐ: \(\sqrt{x-1}>0\)
=>x-1>0
=>x>1
Vậy: TXĐ là \(D=\left(1;+\infty\right)\)
g: ĐKXĐ: \(x^2+x-6>0\)
=>\(\left(x+3\right)\left(x-2\right)>0\)
=>\(\left[{}\begin{matrix}x>2\\x< -3\end{matrix}\right.\)
Vậy: TXĐ là \(D=\left(2;+\infty\right)\cup\left(-\infty;-3\right)\)

\(f\left(0\right)=\dfrac{b}{d}\Rightarrow f\left(f\left(0\right)\right)=0\Rightarrow f\left(\dfrac{b}{d}\right)=0\)
\(\Rightarrow\dfrac{\dfrac{ab}{d}+b}{\dfrac{cb}{d}+d}=0\Rightarrow b\left(a+d\right)=0\Rightarrow\left[{}\begin{matrix}b=0\\d=-a\end{matrix}\right.\)
TH1: \(b=0\)
\(f\left(1\right)=1\Rightarrow a=c+d\)
\(f\left(2\right)=2\Rightarrow2a=2\left(2c+d\right)\Rightarrow a=2c+d\)
\(\Rightarrow2c+d=c+d\Rightarrow c=0\) (ktm)
TH2: \(d=-a\)
\(f\left(1\right)=1\Rightarrow a+b=c+d=c-a\Rightarrow2a+b=c\) (1)
\(f\left(2\right)=2\Rightarrow2a+b=2\left(2c+d\right)=2\left(2c-a\right)\Rightarrow4a+b=4c\) (2)
Trừ (2) cho (1) \(\Rightarrow2a=3c\Rightarrow\dfrac{a}{c}=\dfrac{3}{2}\)
\(\Rightarrow\lim\limits_{x\rightarrow\infty}\dfrac{ax+b}{cx+d}=\dfrac{a}{c}=\dfrac{3}{2}\)
Hay \(y=\dfrac{3}{2}\) là tiệm cận ngang

\(f\left(x\right)=\dfrac{x^2-1}{x^2}=1-\dfrac{1}{x^2}\)
\(\int f\left(x\right)dx=\int\left(1-\dfrac{1}{x^2}\right)dx=\int1dx-\int x^{-2}dx\)
=\(x-\dfrac{x^{-2+1}}{-2+1}+C=x-\dfrac{x^{-1}}{-1}+C=x+\dfrac{1}{x}+C\)
C=-1 ta được phương án A(ko tm câu hỏi)
C=0 ta được phương án B(ko tm câu hỏi)
C=2 ta được phương án C(ko tm câu hỏi)
=>chọn D



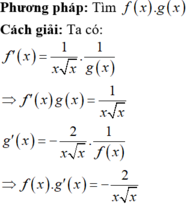
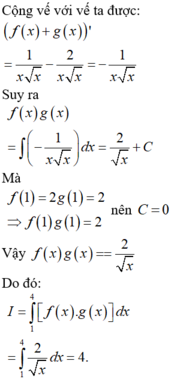
Đáp án B