Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Do \(\left\{{}\begin{matrix}a\ge0\\b\ge1\\a+b+c=5\end{matrix}\right.\) \(\Rightarrow c\le4\)
\(\Rightarrow2\le c\le4\Rightarrow\left(c-2\right)\left(c-4\right)\le0\Rightarrow c^2\le6c-8\)
\(0\le a\le1< 6\Rightarrow a\left(a-6\right)\le0\Rightarrow a^2\le6a\)
\(1\le b\le2< 5\Rightarrow\left(b-1\right)\left(b-5\right)\le0\Rightarrow b^2\le6b-5\)
Cộng vế:
\(a^2+b^2+c^2\le6\left(a+b+c\right)-13=17\)
\(A_{max}=17\) khi \(\left(a;b;c\right)=\left(0;1;4\right)\)
cho ba số dương \(0\le a\le b\le c\le1\) CMR \(\dfrac{a}{bc+1}+\dfrac{b}{ac+1}+\dfrac{c}{ab+1}\le2\)

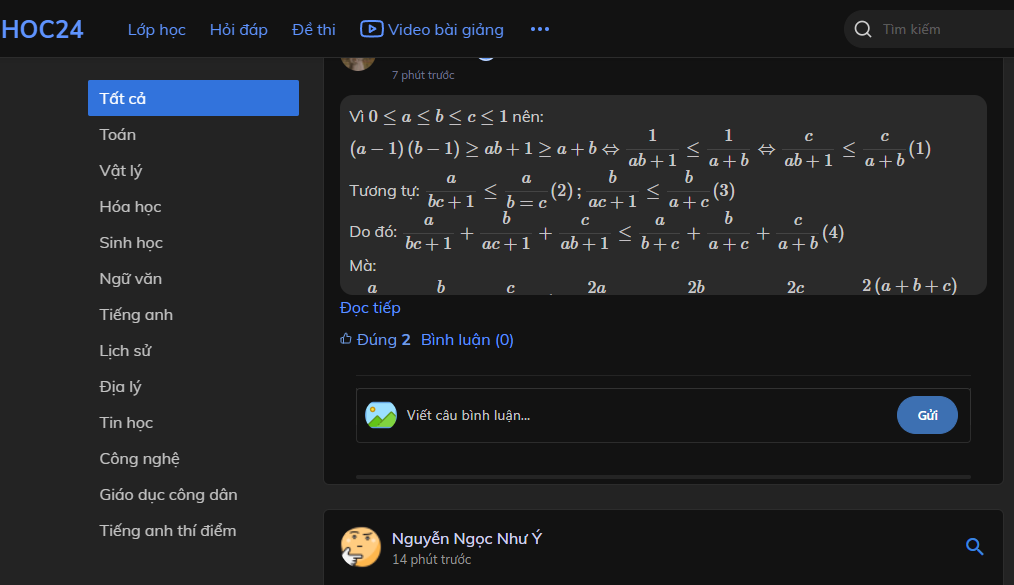
Vì \(0\le a\le b\le c\le1\) nên:
\(\left(a-1\right)\left(b-1\right)\ge ab+1\ge a+b\Leftrightarrow\dfrac{1}{ab+1}\le\dfrac{1}{a+b}\Leftrightarrow\dfrac{c}{ab+1}\le\dfrac{c}{a+b}\left(1\right)\)
Tương tự: \(\dfrac{a}{bc+1}\le\dfrac{a}{b=c}\left(2\right);\dfrac{b}{ac+1}\le\dfrac{b}{a+c}\left(3\right)\)
Do đó: \(\dfrac{a}{bc+1}+\dfrac{b}{ac+1}+\dfrac{c}{ab+1}\le\dfrac{a}{b+c}+\dfrac{b}{a+c}+\dfrac{c}{a+b}\left(4\right)\)
Mà: \(\dfrac{a}{b+c}+\dfrac{b}{a+c}+\dfrac{c}{a+b}\le\dfrac{2a}{a+b+c}+\dfrac{2b}{a+b+c}+\dfrac{2c}{a+b+c}=\dfrac{2\left(a+b+c\right)}{a+b+c}=2\left(5\right)\)
Từ (4) và (5) suy ra \(\dfrac{a}{bc+1}+\dfrac{b}{ac+1}+\dfrac{c}{ab+1}\left(đpcm\right)\)

a) Áp dụng bất đẳng thức Bnhiacopxki ta có :
\(\left(1^2+1^2+1^2\right)\left(a^2+b^2+c^2\right)\ge\left(a.1+b.1+c.1\right)^2\)
\(\Leftrightarrow3\left(a^2+b^2+c^2\right)\ge\left(a+b+c\right)^2\)
\(\Rightarrow a^2+b^2+c^2\ge\frac{\left(a+b+c\right)^2}{3}=\frac{3^2}{3}=3\)
b) Ta có : \(\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2\ge0\)(đúng)
\(\Leftrightarrow2a^2+2b^2+2c^2-2ab-2bc-2ac\ge0\)
\(\Leftrightarrow a^2+b^2+c^2\ge ab+ac+bc\)
\(\Leftrightarrow a^2+b^2+c^2+2ab+2bc+2ac\ge3ab+3bc+3ac\)
\(\Leftrightarrow\left(a+b+c\right)^2\ge3\left(ab+ac+bc\right)\)
\(\Rightarrow ab+ac+bc\le\frac{\left(a+b+c\right)^2}{3}=\frac{3^2}{3}=3\)

$a(a-1)\leq 0 <=> a^2\leq 0 => \sum a^2 \leq \sum a$
$(a-1)(b-1)(c-1)\leq 0 <=> a+b+c-\sum ab +abc -1 \leq 0$
$<=> \sum a^2 -\sum ab \leq a+b+c-\sum ab \leq 1-abc\leq 1$
^^ Mong olm dịch đ.c tatex mình ghi :v


\(P=a\left(1-b\right)+b\left(1-c\right)+c\left(1-a\right)\)
Do \(0\le a;b;c\le1\Rightarrow P\ge0\)
Dấu "=" xảy ra khi \(\left(a;b;c\right)=\left(0;0;0\right);\left(1;1;1\right)\) và có thể những giá trị khác làm biếng ko tìm :D
Bạn có sai đề ko chứ nếu MAX thì mk làm đc