Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Từ giả thiết
2017 1 − y 2017 x = x 2 + 2018 1 − y 2 + 2018 ⇔ 2017 1 − y 1 − y 2 + 2018 = 2017 x x 2 + 2018 *
Xét hàm số f t = 2017 t t 2 + 2018 với t ∈ 0 ; 1
⇒ f ' t = 2017 t ln 2017 t 2 + 2018 + 2 t .2017 t > 0
⇒ f t đồng biến trên 0 ; 1 . Do đó (*) ⇔ 1 − y = x ⇔ x + y = 1.
Ta có: 0 ≤ x y ≤ x + y 2 4 = 1 4 . Đặt m = x y ∈ 0 ; 1 4 . Khi đó :
S = 16 x 2 y 2 + 34 x y + 12 y + x y + x 2 − 3 x y = 16 m 2 − 2 m + 12 = g m
Xét hàm g m trên đoạn
0 ; 1 4 ⇒ g ' m = 32 m − 2 → g ' m = 0 ⇔ m = 1 16
Lúc này
g 0 = 12 , g 1 4 = 25 2 , g 1 16 = 191 16 ⇒ M = 25 2 m = 191 16 ⇒ M + m = 391 16 .

Đáp án C
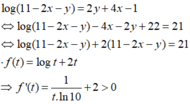
Suy ra f(t) đồng biến trên TXĐ và pt f(t) = 21 chỉ có 1 nghiệm duy nhất
Ta thấy t = 10 là 1 nghiệm của pt nên t = 10 là nghiệm duy nhất của pt
⇒ 11 − 2 x − y = 10 ⇒ y = 1 − 2 x ⇒ P = 16 x 2 ( 1 − 2 x ) − 2 x ( 3 − 6 x + 2 ) − 1 + 2 x + 5 = − 32 x 3 + 28 x 2 − 8 x + 4 P ' = − 96 x 2 + 56 x − 8 P ' = 0 ⇔ x = 1 4 x = 1 3 P ( 0 ) = 4 , P ( 1 3 ) = 88 27 , P ( 1 4 ) = 13 4 , P ( 1 2 ) = 3 ⇒ m = 13 4 , M = 4 ⇒ M + 4 m = 17

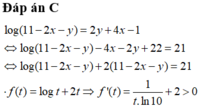
Suy ra f(t) đồng biến trên TXĐ và pt f ( t ) = 21 chỉ có 1 nghiệm duy nhất
Ta thấy t = 10 là 1 nghiệm của pt nên t = 10 là nghiệm duy nhất của pt
⇒ 11 - 2 x - y = 10 ⇒ y = 1 - 2 x ⇒ P = 16 x 2 1 - 2 x - 2 x 3 - 6 x + 2 - 1 + 2 x + 5 = - 32 x 3 + 28 x 2 - 8 x + 4 P ' = - 96 x 2 + 56 x - 8 P ' = 0 ⇔ [ x = 1 4 x = 1 3 P 0 = 4 , P 1 3 = 88 27 , P 1 4 = 13 4 , P 1 2 = 3 ⇒ m = 13 4 , M = 4 ⇒ M + 4 m = 17

Đáp án C
Ta có x + y = 3 ⇒ y = 3 − x ≥ 1 ⇔ x ≤ 2 ⇒ x ∈ 0 ; 2
Khi đó P = f x = x 3 + 2 3 − x 2 + 3 x 2 + 4 x 3 − x − 5 x = x 3 + x 2 − 5 x + 18
Xét hàm số f x = x 3 + x 2 − 5 x + 18 trên đoạn 0 ; 2 , có f ' x = 3 x 2 + 2 x − 5
Phương trình 0 ≤ x ≤ 2 3 x 2 + 2 x − 5 = 0 ⇔ x = 1. Tính f 0 = 18 , f 1 = 15 , f 2 = 20
Vậy min 0 ; 2 f x = 15 , m a x 0 ; 2 f x = 20 hay P m a x = 20 và P min = 15

Chọn đáp án B
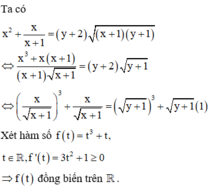
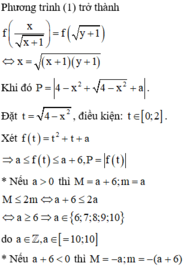
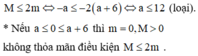
Vậy có 5 giá trị nguyên của m thỏa mãn điều kiện.

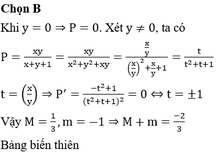
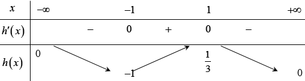


Đáp án B
Ta có 2017 1 − x − y = x 2 + 2018 y 2 − 2 y + 2019 ⇔ 2017 1 − y 2017 x = x 2 + 2018 1 − y 2 + 2018
2017 x x 2 + 2018 = 2017 1 − y 1 − y 2 + 2018 ⇔ f x = f 1 − y
Xét hàm số f t = 2017 t t 2 + 2018 = t 2 .2017 t + 2018.2017 t , có
f ' t = 2 t .2017 t + t 2 .2017 t . ln 2017 + 2018.2017 t . ln 2017 > 0 ; ∀ t > 0
Suy ra f(t) là hàm đồng biến trên 0 ; + ∞ mà f x = f 1 − y ⇒ x + y = 1
Lại có P = 4 x 2 + 3 y 4 y 2 + 3 x + 25 x y = 16 x 2 y 2 + 12 x 3 + 12 y 3 + 34 x y
16 x 2 y 2 + 12 x + y 3 − 3 x y x + y + 34 x y = 16 x 2 y 2 + 12 1 − 3 x y + 34 x y = 16 x 2 y 2 − 2 x y + 12
Mà 1 = x + y ≥ 2 x y ⇔ x y ≤ 1 4 nên đặt t = x y ∈ 0 ; 1 4 khi đó P = f t = 16 t 2 − 2 t + 12
Xét hàm số f t = 16 t 2 − 2 y + 12 trên 0 ; 1 4 ta được min 0 ; 1 4 f t = f 1 16 = 191 16 max 0 ; 1 4 f t = f 1 4 = 25 2