Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



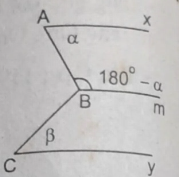
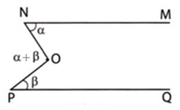
a) Ta có: \(\alpha+\widehat{ABm}=\alpha+180^0-\alpha=180^0\)
Mà 2 góc này là 2 góc trong cùng phía
=> Ax//Bm
b) Trên tia đối Bm kẻ Bn
=> Bn//Ax
\(\Rightarrow\alpha=\widehat{ABn}\)(so le trong)
\(\Rightarrow\widehat{CBn}=\widehat{ABC}-\widehat{ABn}=\alpha+\beta-\alpha=\beta\)
\(\Rightarrow\widehat{CBn}=\widehat{BCy}=\beta\)
Mà 2 góc này là 2 góc so le trong
=> Cy//Bm

A= 11 1 + 12 1 +...+ 70 1 A = ( 1 11 + 1 12 + . . . + 1 20 ) + ( 1 21 + 1 22 + . . . + 1 30 ) A=( 11 1 + 12 1 +...+ 20 1 )+( 21 1 + 22 1 +...+ 30 1 ) + ( 1 31 + 1 32 + . . . + 1 40 ) + ( 1 41 + 1 42 + . . . + 1 50 ) + ( 1 51 + 1 52 + . . . + 1 60 ) +( 31 1 + 32 1 +...+ 40 1 )+( 41 1 + 42 1 +...+ 50 1 )+( 51 1 + 52 1 +...+ 60 1 ) + ( 1 61 + 1 62 + . . . + 1 70 ) +( 61 1 + 62 1 +...+ 70 1 ) ⇒ A < 1 10 ⋅ 10 + 1 20 ⋅ 10 + 1 30 ⋅ 10 + . . . + 1 60 ⋅ 10 ⇒A< 10 1 ⋅10+ 20 1 ⋅10+ 30 1 ⋅10+...+ 60 1 ⋅10 A < 1 + 1 2 + 1 3 + . . . + 1 6 A<1+ 2 1 + 3 1 +...+ 6 1 A < 1 + 1 2 + 1 3 + 1 6 + ( 1 4 + 1 5 ) A<1+ 2 1 + 3 1 + 6 1 +( 4 1 + 5 1 ) A < 2 + 0 , 45 < 2 , 5 A<2+0,45<2,5
Đây qu, phiền bạn tick giup mình nha
A=111+121+...+701
\(A = \left(\right. \frac{1}{11} + \frac{1}{12} + . . . + \frac{1}{20} \left.\right) + \left(\right. \frac{1}{21} + \frac{1}{22} + . . . + \frac{1}{30} \left.\right)\)
\(+ \left(\right. \frac{1}{31} + \frac{1}{32} + . . . + \frac{1}{40} \left.\right) + \left(\right. \frac{1}{41} + \frac{1}{42} + . . . + \frac{1}{50} \left.\right) + \left(\right. \frac{1}{51} + \frac{1}{52} + . . . + \frac{1}{60} \left.\right)\)
\(+ \left(\right. \frac{1}{61} + \frac{1}{62} + . . . + \frac{1}{70} \left.\right)\)
\(\Rightarrow A < \frac{1}{10} \cdot 10 + \frac{1}{20} \cdot 10 + \frac{1}{30} \cdot 10 + . . . + \frac{1}{60} \cdot 10\)
\(A < 1 + \frac{1}{2} + \frac{1}{3} + . . . + \frac{1}{6}\)
\(A < 1 + \frac{1}{2} + \frac{1}{3} + \frac{1}{6} + \left(\right. \frac{1}{4} + \frac{1}{5} \left.\right)\)
\(A < 2 + 0 , 45 < 2 , 5\)

Bài làm
a) x4+x3+2x2+x+1=(x4+x3+x2)+(x2+x+1)=x2(x2+x+1)+(x2+x+1)=(x2+x+1)(x2+1)
b)a3+b3+c3-3abc=a3+3ab(a+b)+b3+c3 -(3ab(a+b)+3abc)=(a+b)3+c3-3ab(a+b+c)
=(a+b+c)((a+b)2-(a+b)c+c2)-3ab(a+b+c)=(a+b+c)(a2+2ab+b2-ac-ab+c2-3ab)=(a+b+c)(a2+b2+c2-ab-ac-bc)
c)Đặt x-y=a;y-z=b;z-x=c
a+b+c=x-y-z+z-x=o
đưa về như bài b
d)nhóm 2 hạng tử đầu lại và 2hangj tử sau lại để 2 hạng tử sau ở trong ngoặc sau đó áp dụng hằng đẳng thức dề tính sau đó dặt nhân tử chung
e)x2(y-z)+y2(z-x)+z2(x-y)=x2(y-z)-y2((y-z)+(x-y))+z2(x-y)
=x2(y-z)-y2(y-z)-y2(x-y)+z2(x-y)=(y-z)(x2-y2)-(x-y)(y2-z2)=(y-z)(x2-2y2+xy+xz+yz)