Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: Chiều cao của tháp DC = DC1 + C1C = 1,3 + DC1
=> DC = 1,3 + 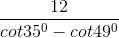
=> DC ≈ 22,8m
cãi đi bé Bài 11 trang 60 sgk hình học 10 - loigiaihay.com

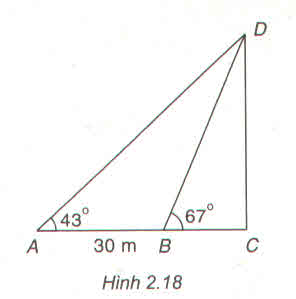
Có:
\(DC=AC.tan43^o=\left(AB+BC\right).tan43^o\).
\(DC=BC.tan67^o\).
Vì vây:
\(\left(AB+BC\right).tan43^o=BC.tan67^o\)
\(\Leftrightarrow BC=\dfrac{AB.tan43^o}{tan67^o-tan43^o}=26,55m\).
Suy ra: \(DC=BC.tan67^o=26,55.tan67^o=62,55m\).
Vậy chiều cao DC của chân tháp là 62,55m.

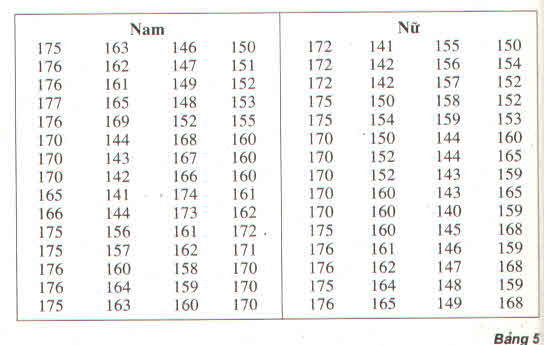
a) Dãy các số liệu chiều cao của các học sinh nam ở bảng 5 có :
\(\overline{x_1}\approx163\left(cm\right);s_1^2\approx134,3;s_1\approx11,59\)
Dãy các số liệu chiều cao của các học sinh nữ cho ở bảng 5 có :
\(\overline{x_2}\approx159,5\left(cm\right);s_2^2\approx148;s_2\approx12,17\)
b) Nhóm T có \(\overline{x_3}=163\left(cm\right);s_3^2=169;s_3=13\)
Học sinh ở nhóm nam và nhóm T có chiều cao như nhau và cùng lớn hơn chiều cao của học sinh ở nhóm nữ (vì \(\overline{x}_1=\overline{x}_3>\overline{x}_2\)
Vì \(\overline{x}_1=\overline{x}_3=163\left(cm\right)\) và \(s_1< s_3\) nên chiều cao của các học sinh nam đồng đều hơn chiều cao của các học sinh nhóm T

Chỉ lm bài thoii, hình bn tự vẽ nha !!!
\(a.\) Tứ giác \(BEDC\) có \(\widehat{BEC}=\widehat{BDC}=90^0\)
Suy ra tứ giác \(BEDC\) là tứ giác nội tiếp
Tam giác \(DBA\) vuông tại \(D\) có đường cao \(DL\) nên suy ra \(BD^2=BL.BA\)
\(b.\) Tứ giác \(ADEH\) có:
\(\widehat{ADH}+\widehat{AEH}=90^0+90^0=180^0\) nên tứ giác \(ADEH\) nội tiếp
Từ đó \(\widehat{BAK}=\widehat{BDE}\)
Mà \(\widehat{BJK}=\widehat{BAK}\) ( 2 góc nội tiếp cùng chắn một cung )
Do đó \(\widehat{BJK}=\widehat{BDE}\)
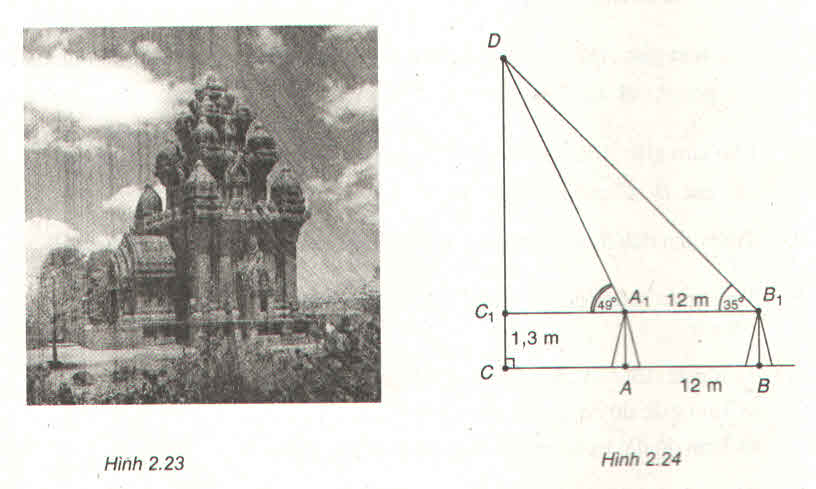
Vì độ chính xác đến hàng trăm (độ chính xác là 0,05) nên ta quy tròn số 41,34 đến hàng phần chục.
Vậy số quy tròn của chiều cao h là 41,3m.
Đáp án C