Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: AM vuông góc BD
=>AM vuông góc (BCD)
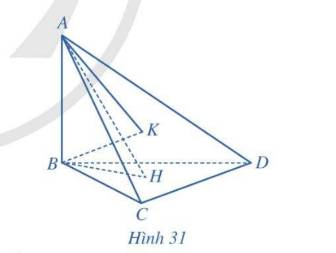
b: Kẻ DK vuông góc BC
=>BK vuông góc BC
(ABD) vuông góc (BCD)
=>DK vuông góc BA
=>(BCD) vuông góc (ABC)
c: AN là giao tuyến chung của (ABC) và (ANM)
=>MH vuông góc AN
=>MH vuông góc (ABC)

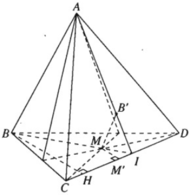
a) MB' qua M và song song với (ABC) và (ABD) ⇒ MB′ song song với giao tuyến AB của hai mặt phẳng này. Ta có: MB′ // AB nên MB' và AB xác định một mặt phẳng. Giả sử MB cắt AB' tại I.
Ta có: I ∈ BM ⇒ I ∈ (BCD)
I ∈ AB′ ⇒ I ∈ (ACD)
Nên I ∈ (BCD) ∩ (ACD) = CD
Có: I ∈ CD
Vậy ba đường thẳng AB', BM và CD đồng quy tại I.
b) MB′ // AB 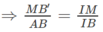
Kẻ MM′ ⊥ CD và BH ⊥ CD
Ta có: MM′ // BH 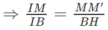
Mặt khác:
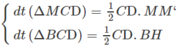
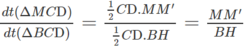
Do đó: 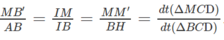
Vậy 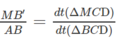
c) Tương tự ta có: 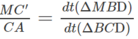
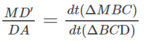
Vậy:
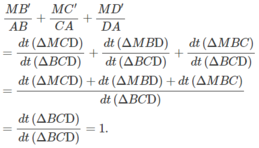


a) Xét tam giác ABC cân tại A có
I là trung điểm của BC
\( \Rightarrow AI \bot BC\)
Xét tam giác ACD cân tại D có
I là trung điểm của BC
\( \Rightarrow DI \bot BC\)
Ta có \(AI \bot BC,DI \bot BC \Rightarrow BC \bot \left( {AID} \right)\)
b) \(BC \bot \left( {AID} \right);BC \subset \left( {BCD} \right) \Rightarrow \left( {BCD} \right) \bot \left( {AID} \right)\)
\(\left( {BCD} \right) \cap \left( {AID} \right) = DI\)
Trong (AID) có \(AH \bot DI\)
\( \Rightarrow AH \bot \left( {BCD} \right)\)
c) Ta có \(BC \bot \left( {AID} \right);IJ \subset \left( {AID} \right) \Rightarrow BC \bot IJ\)
Mà \(IJ \bot AD\)
Do đó IJ là đường vuông góc chung của AD và BC.

a) Vì \(AB \bot \left( {BCD} \right) \Rightarrow AB \bot CD\left( 1 \right)\)
Có H là trực tâm của tam giác BCD \( \Rightarrow BH \bot CD\left( 2 \right)\)
Tử (1) và (2) \( \Rightarrow CD \bot \left( {ABH} \right)\)
b) Vì \(AB \bot \left( {BCD} \right) \Rightarrow AB \bot CD\left( 1 \right)\)
Có K là trực tâm của tam giác BCD \( \Rightarrow AK \bot CD\left( 2 \right)\)
Từ (1) và (2) \( \Rightarrow CD \bot \left( {ABK} \right)\)

a/ \(AB\perp\left(BCD\right)\Rightarrow AB\perp CD\)
Mà \(BE\perp CD\Rightarrow CD\perp\left(ABE\right)\)
\(CD\in\left(ACD\right)\Rightarrow\left(ACD\right)\perp\left(ABE\right)\)
*/ \(AB\perp\left(BCD\right)\Rightarrow AB\perp DF\)
\(DF\perp BC\Rightarrow DF\perp\left(ABC\right)\Rightarrow DF\perp AC\)
Mà \(AC\perp DK\Rightarrow AC\perp\left(DFK\right)\Rightarrow\left(ACD\right)\perp\left(DFK\right)\)
b/ H là trực tâm ACD \(\Rightarrow CD\perp AH\)
Mà \(CD\perp AB\Rightarrow CD\perp\left(ABE\right)\)
\(\Rightarrow CD\perp OH\)
Theo câu a ta có \(AC\perp\left(DFK\right)\Rightarrow AC\perp OH\)
\(\Rightarrow OH\perp\left(ACD\right)\)

Trong (BCD): DG \cap∩ BC = F
Vậy DG \cap∩ (ABC) = F.
b. Cách 1: MG \subset⊂ (BMG) \equiv≡ (ABH) (H = BG \cap∩ DC)
(Do mặt phẳng (BMG) "lơ lửng" trong hình chóp nên ta kéo dài BM thành BA và BG thành BH để ta có cái nhìn dễ dàng hơn đối với mặt phẳng này).
(BMG) \cap∩ (ACD) =AH
Trong (ABH): MG \cap∩ AH =K
Vậy MG \cap∩ (ACD) = K.
a. Trong (BCD) có GD và BC cắt nhau tại K
vậy K = GD và (ABC)
b. có MG ⊂ (BMG) trùng (ABH) có H = BG và DC
(BMG) và (ACD) = AH
Trong (ABH) có MG và AH = P
Vậy MG và (ACD) = P