Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
em mình không biết làm bài này nên nhờ mọi người giải hộ mình nha
\(a.\frac47-\frac47:\frac{5}{14}=\frac47-\frac47\cdot\frac{14}{5}\)
\(=\frac47\cdot\left(1-\frac{14}{5}\right)=\frac47\cdot\left(-\frac95\right)=-\frac{36}{35}\)
\(b.\left(-\frac57\right)^2+8\cdot\left(0,5\right)^3+\left(-1\right)^{2025}=\frac{25}{49}+8\cdot0,125-1\)
\(=\frac{25}{49}+1-1=\frac{25}{49}\)
\(c.\left(1-\frac35\right)^2-\left(-\frac34\right)+\left(-\frac{13}{10}\right)=\left(\frac25\right)^2+\frac34-\frac{13}{10}\)
\(=\frac{4}{25}+\frac34-\frac{13}{10}=\frac{16}{100}+\frac{75}{100}-\frac{130}{100}=\frac{16+75-130}{100}=-\frac{39}{100}\)
\(d.\left(-\frac35+\frac49\right):\frac{7}{11}+\left(-\frac25+\frac59\right):\frac{7}{11}=-\frac{7}{45}\cdot\frac{11}{7}+\frac{7}{45}\cdot\frac{11}{7}\)
\(=\frac{11}{7}\cdot\left(\frac{7}{45}-\frac{7}{45}\right)=\frac{11}{7}\cdot0=0\)
Ta có:
\(\hat{Q_3}\) = \(\hat{Q_1}\)(đối đỉnh)
⇒ \(\hat{Q}_1\) = \(\hat{P_1}\) (tính chất bác cầu) (1)
Hai góc \(Q_1\) và \(P_1\) ở vị trí đồng vị (2)
Từ 1 và (2) ta có:
m//n (đpcm)
Giải:
a; m ⊥ d; n ⊥ d
⇒ m//n (hai đường thẳng cùng vuông góc với đường thẳng thứ ba thì song song với nhau)
b; Điểm B trên hình đâu em?
Giải:
a; \(\hat{x^{\prime}AB}\) = \(\hat{ABy}\) = 70\(^0\)(gt) (1)
\(\hat{x^{\prime}AB}\) và \(\hat{ABy}\) (hai góc so le trong) (2)
Kết hợp (1) và (2) ta có:
\(xx^{\prime}\) // yy'
b; \(xx^{\prime}\) // yy' (cmt) (a)
mm' ⊥ \(x\)\(x^{\prime}\)(gt) (b)
Từ (a) và (b) ta có:
mm'⊥ yy' (tính chất từ vuông góc đến song song)
⇒ \(\hat{yDm^{\prime}}\) = 90\(^0\)
Bài 14:
\(A\left(x\right)+B\left(x\right)=5x^4-6x^3-3x^2-4\)
\(A\left(x\right)-B\left(x\right)=3x^4+7x^2+8x+2\)
Do đó: \(A\left(x\right)+B\left(x\right)+A\left(x\right)-B\left(x\right)=5x^4-6x^3-3x^2-4+3x^4+7x^2+8x+2\)
=>\(2\cdot A\left(x\right)=8x^4-6x^3+4x^2+8x-2\)
=>\(A\left(x\right)=4x^4-3x^3+2x^2+4x-1\)
Ta có: \(A\left(x\right)+B\left(x\right)=5x^4-6x^3-3x^2-4\)
=>\(B\left(x\right)=5x^4-6x^3-3x^2-4-4x^4+3x^3-2x^2-4x-1\)
=>\(B\left(x\right)=x^4-3x^3-5x^2-4x-5\)
Bài 13:
\(f\left(x\right)+g\left(x\right)=6x^4-3x^2-5\)
\(f\left(x\right)-g\left(x\right)=4x^4-6x^3+7x^2+8x-9\)
Do đó: \(f\left(x\right)+g\left(x\right)+f\left(x\right)-g\left(x\right)=6x^4-3x^2-5+4x^4-6x^3+7x^2+8x-9\)
=>\(2\cdot f\left(x\right)=10x^4-6x^3+4x^2+8x-14\)
=>\(f\left(x\right)=5x^4-3x^3+2x^2+4x-7\)
\(f\left(x\right)+g\left(x\right)=6x^4-3x^2-5\)
=>\(g\left(x\right)=6x^4-3x^2-5-5x^4+3x^3-2x^2-4x+7=x^4+3x^3-5x^2-4x+2\)
\(\hat{N_2}\) = \(\hat{N_4}\) (hai góc đối đỉnh)
⇒ \(\hat{M_1}\) = \(\hat{N_4}\) (tính chất bác cầu) (1)
Góc \(\hat{N_1}\) và \(\hat{M_4}\) (hai góc đồng vị) (2)
Từ (1) và (2) ta có:
c // d (đpcm)
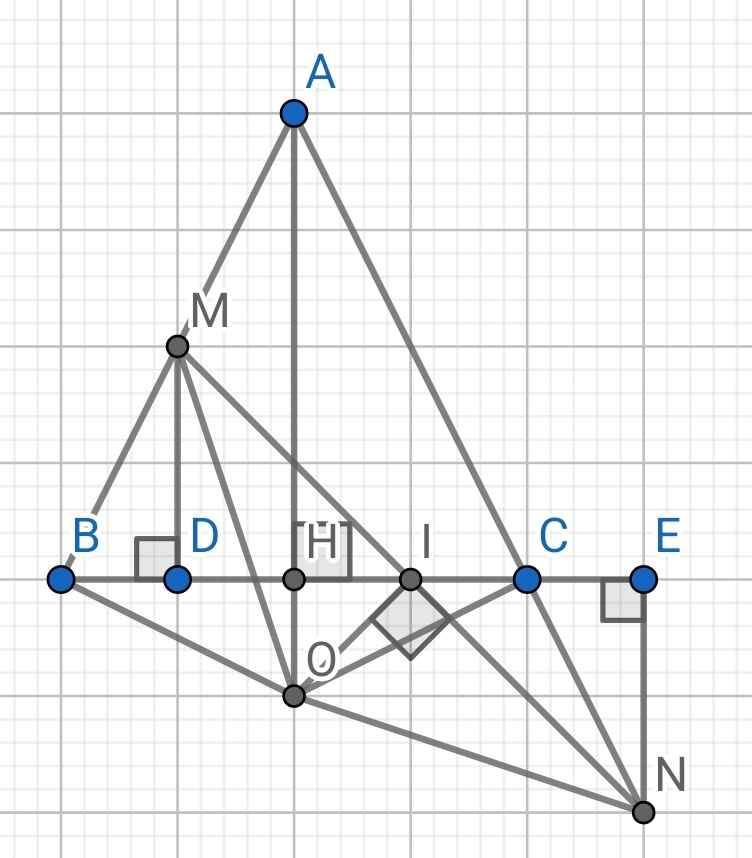a) ∆ABC cân tại A
⇒ ∠ABC = ∠ACB
Mà ∠ACB = ∠ECN (đối đỉnh)
⇒ ∠ABC = ∠ECN
⇒ ∠DBM = ∠ECN
Xét hai tam giác vuông: ∆DBM và ∆ECN có:
BD = CE (gt)
∠DBM = ∠ECN (cmt)
⇒ ∆DBM = ∆ECN (cạnh góc vuông - góc nhọn kề)
⇒ DM = EN (hai cạnh tương ứng)
b) Do DM ⊥ BC (gt)
EN ⊥ BC (gt)
⇒ DM // EN
⇒ ∠DMI = ∠ENI (so le trong)
Xét hai tam giác vuông: ∆DMI và ∆ENI có:
DM = EN (cmt)
∠DMI = ∠ENI (cmt)
⇒ ∆DMI = ∆ENI (cạnh góc vuông - góc nhọn kề)
⇒ MI = NI (hai cạnh tương ứng)
⇒ I là trung điểm của MN
⇒ BC cắt MN tại trung điểm I của MN
c) Do AH ⊥ BC nên AH là đường cao của ∆ABC
Mà ∆ABC cân tại A
AH cũng là đường phân giác của ∆ABC
⇒ ∠BAH = ∠CAH
⇒ ∠BAO = ∠CAO
Do ∆ABC cân tại A (gt)
⇒ AB = AC
Xét ∆OAB và ∆OAC có:
OA là cạnh chung
∠BAO = ∠CAO (cmt)
AB = AC (cmt)
⇒ ∆OAB = ∆OAC (c-g-c)
⇒ OB = OC (hai cạnh tương ứng)
Ta có:
I là trung điểm MN (cmt)
OI ⊥ MN (gt)
⇒ OI là đường trung trực của MN
⇒ OM = ON
Do ∆DBM = ∆ECN (cmt)
⇒ BM = CN (hai cạnh tương ứng)
Xét ∆OBM và ∆OCN có:
OB = OC (cmt)
OM = ON (cmt)
BM = CN (cmt)
⇒ ∆OBM = ∆OCN (c-c-c)
d) Do ∆OBM = ∆OCN (cmt)
⇒ ∠OBM = ∠OCN (hai góc tương ứng)
Do ∆OAB = ∆OAC (cmt)
⇒ ∠OBA = ∠OCA (hai góc tương ứng)
⇒ ∠OBM = ∠OCA
Mà ∠OBM = ∠OCN (cmt)
⇒ ∠OCN = ∠OCA
Mà ∠OCN + ∠OCA = 180⁰ (kề bù)
⇒ ∠OCN = ∠OCA = 180⁰ : 2 = 90⁰
⇒ OC ⊥ AC
a) ∆ABC cân tại A
⇒ ∠ABC = ∠ACB
Mà ∠ACB = ∠ECN (đối đỉnh)
⇒ ∠ABC = ∠ECN
⇒ ∠DBM = ∠ECN
Xét hai tam giác vuông: ∆DBM và ∆ECN có:
BD = CE (gt)
∠DBM = ∠ECN (cmt)
⇒ ∆DBM = ∆ECN (cạnh góc vuông - góc nhọn kề)
⇒ DM = EN (hai cạnh tương ứng)
b) Do DM ⊥ BC (gt)
EN ⊥ BC (gt)
⇒ DM // EN
⇒ ∠DMI = ∠ENI (so le trong)
Xét hai tam giác vuông: ∆DMI và ∆ENI có:
DM = EN (cmt)
∠DMI = ∠ENI (cmt)
⇒ ∆DMI = ∆ENI (cạnh góc vuông - góc nhọn kề)
⇒ MI = NI (hai cạnh tương ứng)
⇒ I là trung điểm của MN
⇒ BC cắt MN tại trung điểm I của MN
c) Do AH ⊥ BC nên AH là đường cao của ∆ABC
Mà ∆ABC cân tại A
AH cũng là đường phân giác của ∆ABC
⇒ ∠BAH = ∠CAH
⇒ ∠BAO = ∠CAO
Do ∆ABC cân tại A (gt)
⇒ AB = AC
Xét ∆OAB và ∆OAC có:
OA là cạnh chung
∠BAO = ∠CAO (cmt)
AB = AC (cmt)
⇒ ∆OAB = ∆OAC (c-g-c)
⇒ OB = OC (hai cạnh tương ứng)
Ta có:
I là trung điểm MN (cmt)
OI ⊥ MN (gt)
⇒ OI là đường trung trực của MN
⇒ OM = ON
Do ∆DBM = ∆ECN (cmt)
⇒ BM = CN (hai cạnh tương ứng)
Xét ∆OBM và ∆OCN có:
OB = OC (cmt)
OM = ON (cmt)
BM = CN (cmt)
⇒ ∆OBM = ∆OCN (c-c-c)
d) Do ∆OBM = ∆OCN (cmt)
⇒ ∠OBM = ∠OCN (hai góc tương ứng)
Do ∆OAB = ∆OAC (cmt)
⇒ ∠OBA = ∠OCA (hai góc tương ứng)
⇒ ∠OBM = ∠OCA
Mà ∠OBM = ∠OCN (cmt)
⇒ ∠OCN = ∠OCA
Mà ∠OCN + ∠OCA = 180⁰ (kề bù)
⇒ ∠OCN = ∠OCA = 180⁰ : 2 = 90⁰
⇒ OC ⊥ AC
