chi ti
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
18 tháng 3 2023
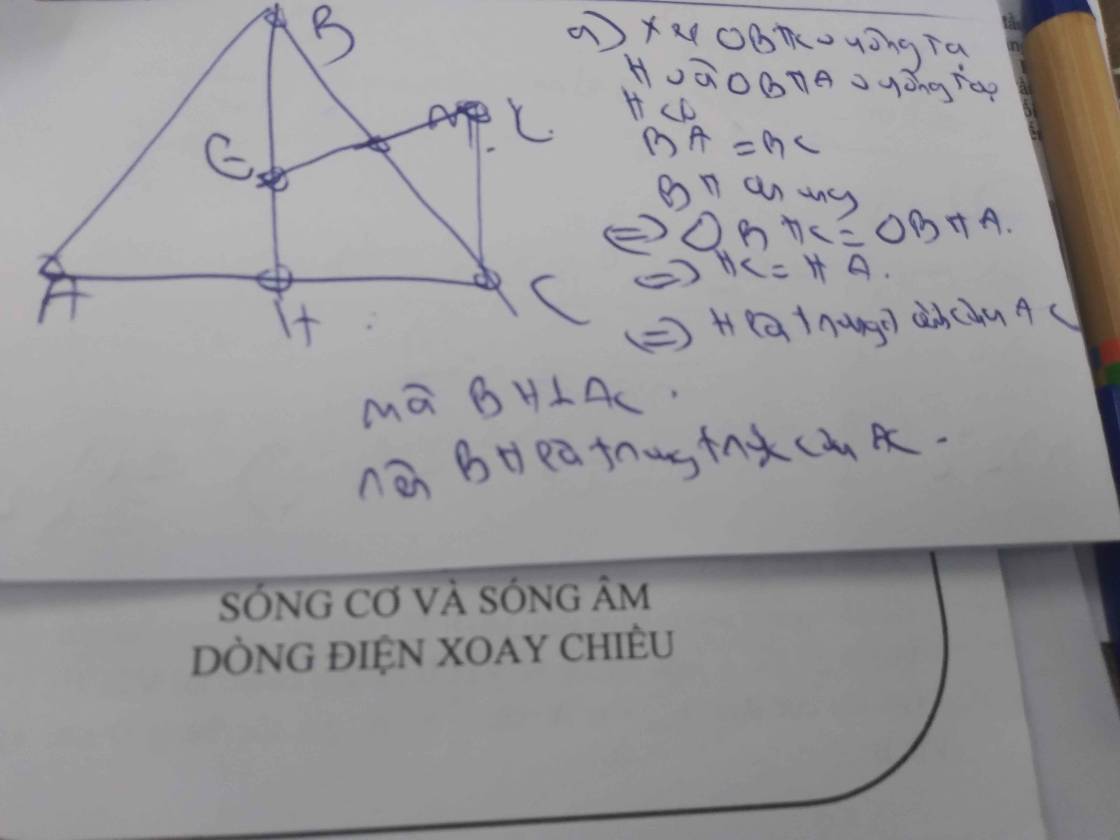
a: XetΔBAD vuông tại A và ΔBHD vuông tại H có
BD chung
góc ABD=góc HBD
=>ΔBAD=ΔBHD
=>BA=BH; DA=DH
mà DH<DC
nên DA<DC
b: Xét ΔBHK vuông tại H và ΔBAC vuông tại A có
BH=BA
góc B chung
=>ΔBHK=ΔBAC
=>BK=BC
c: ΔBKC cân tại B
mà BD là phân giác
nên BD là trung trực của KC
26 tháng 12 2021
a: Ta có: ΔBDC cân tại B
mà BI là đường phân giác
nên I là trung điểm của CD
hay IC=ID
5 tháng 11 2021
Ta có \(\widehat{S}+\widehat{SGQ}+\widehat{Q}=180^0\Rightarrow\widehat{S}+\widehat{Q}=180^0-\widehat{SGQ}\)
Mà \(\widehat{S}-\widehat{Q}=12^0\Rightarrow\left\{{}\begin{matrix}\widehat{S}=\dfrac{180^0-\widehat{SGQ}+12^0}{2}=96^0-\dfrac{\widehat{SGQ}}{2}\\\widehat{Q}=\dfrac{180^0-\widehat{SGQ}-12^0}{2}=84^0-\dfrac{\widehat{SGQ}}{2}\end{matrix}\right.\)
Mà GP là p/g nên \(\widehat{QGP}=\widehat{PGS}=\dfrac{\widehat{SGQ}}{2}\)
\(\Rightarrow\widehat{Q}=84^0-\widehat{QGP}\)
Ta có \(\widehat{GPS}=\widehat{Q}+\widehat{QGP}=84^0-\widehat{QGP}+\widehat{QGP}=84^0\) (tc góc ngoài)
30 tháng 6 2023
a: Xét ΔMEI vuông tại M và ΔHEI vuông tại H có
EI chung
góc MEI=góc HEI
=>ΔMEI=ΔHEI
b: EM=EH và IM=IH
=>EI là trung trực của MH
c: góc MIE=góc FIK=60 độ
=>góc FKI=30 độ
Xét ΔHKI vuông tại H và ΔFKI vuông tại F có
KI chung
góc HKI=góc FKI
=>ΔHKI=ΔFKI
=>KH=KF
Xét ΔIEK có góc IEK=góc IKE
nên ΔIEK cân tại I
mà IH là đường cao
nên H là trung điểm của EK
=>HE=KH=FK
d: IK=IE
IE>IM
=>IK>IM
e: Gọi A là giao của FK và EM
Xét ΔEAK có
EF,KM là đường cao
EF cắt KM tại I
=>I là trực tâm
=>AI vuông góc EK
=>A,I,H thẳng hàng
=>EM,Hi,KF đồng quy
30 tháng 6 2023
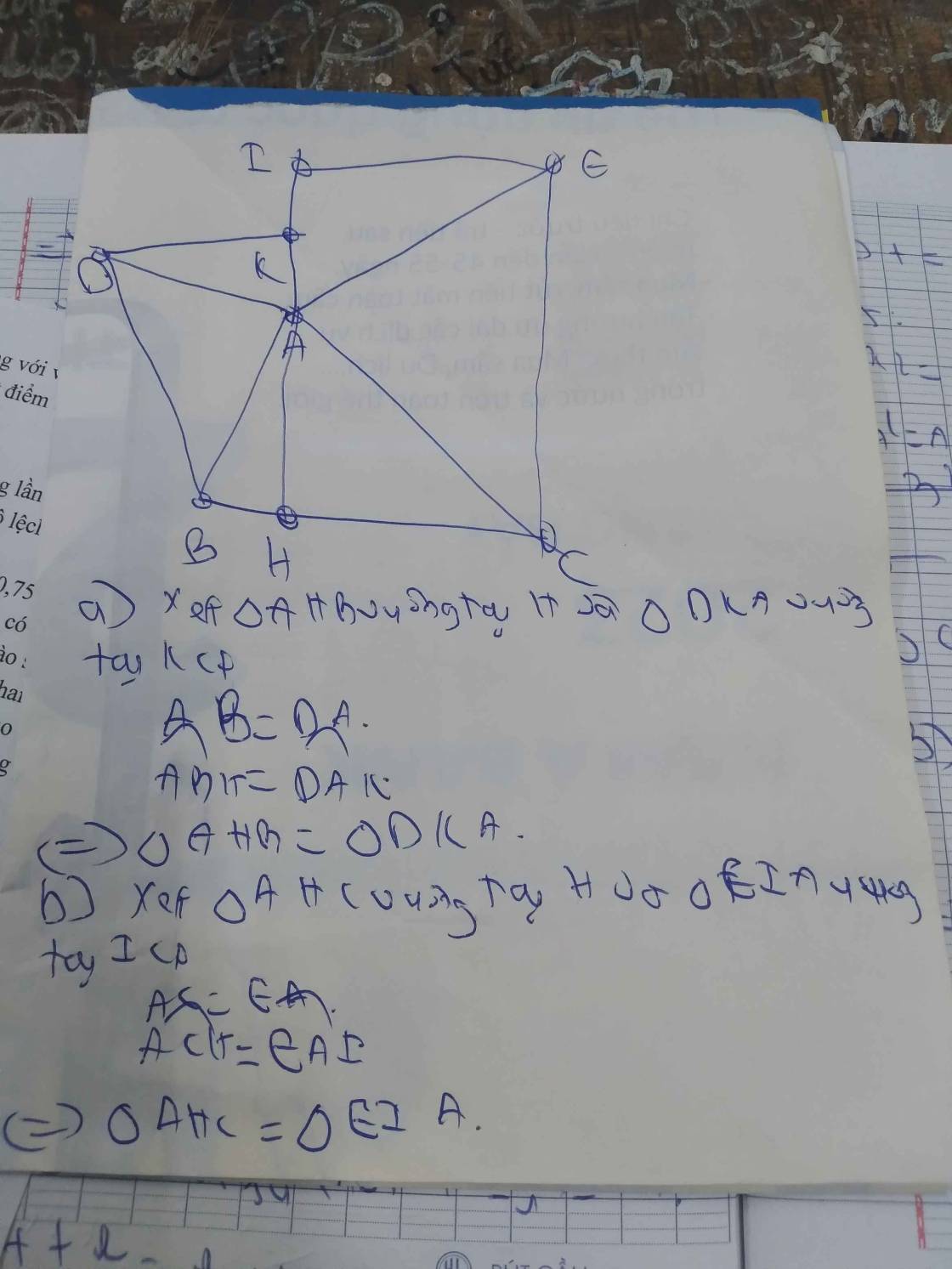
a: Xét ΔBAH và ΔBDH có
BA=BD
AH=DH
BH chung
=>ΔBAD=ΔBDH
b: Xét ΔBAE và ΔBDE có
BA=BD
góc ABE=góc DBE
BE chung
=>ΔBAE=ΔBDE
=>EA=ED và góc BDE=góc BAE=90 độ
=>ΔEAD cân tại E và DE vuông góc BC
c: ED=EA
EA<EM
=>EM>ED
d: Xét ΔBDM vuông tại D và ΔBAC vuông tại A có
BD=BA
góc DBM chung
=>ΔBDM=ΔBAC
=>BM=BC
=>ΔBMC cân tại B
mà BK là trung tuyến
nên BK là phân giác của góc ABC
=>B,E,K thẳng hàng
12 tháng 1 2023
Bài 1:
a,b: ΔABC cân tại A
mà AM là trung tuyến
nên AM vừa là đường cao, vừa là phân giác
=>góc BAM=góc CAM và AM vuông góc với BC
c: Xét ΔEBC có
EM vừa là đường cao, vừa là trung tuyến
nên ΔEBC cân tại E
d: Xét ΔKCB có
CE là trung tuyến
CE=KB/2
Do đó: ΔKCB vuông tại C
=>KC//AE
a: Xét ΔCDB có
CA vừa là đường cao, vừa là trung tuyến
=>ΔCDB cân tại C
=>CA là phân giác của góc DCB
b: Xét ΔCMH vuông tại M và ΔCNH vuông tại N có
CH chung
góc MCH=góc NCH
=>ΔCMH=ΔCNH
=>CM=CN
=>ΔCMN cân tại C
Xét ΔCDB có CM/CD=CN/CB
nên MN//DB
c: HB>HN
HM=HN
=>HB>HM