Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a/
Ta có
\(AB\perp AC\Rightarrow AD\perp AC;HE\perp AC\) => AD//HE
\(AC\perp AB\Rightarrow AE\perp AB,HD\perp AB\) => AE//HD
=> ADHE là hbh (Tứ giác có các cặp cạnh đối // với nhau từng đôi một là hbh)
Mà \(\widehat{A}=90^o\)
=> ADHE là hình CN
b/
Xét tg vuông ADH có
\(DH=\sqrt{AH^2-AD^2}\) (Pitago)
\(\Rightarrow DH=\sqrt{5^2-4^2}=3cm\)
\(\Rightarrow S_{ADHE}=AD.DH=4.3=12cm^2\)
c/
Ta có
DB=DI (gt); DH=DK (gt) => BKIH là hbh (Tứ giác có 2 đường chéo cắt nhau tại trung điểm mỗi đường là hbh)
Xét tg AKH có
\(HD\perp AB\Rightarrow AD\perp HK\) (1)
BKIH là hình bình hành (cmt) => KI//BH (cạn đối hbh)
Mà \(AH\perp BC\left(gt\right)\Rightarrow BH\perp AH\)
\(\Rightarrow KI\perp AH\) (2)
Từ (1) và (2) => I là trực tâm của tg AKH => \(AK\perp HI\) (trong tg 3 đường cao đồng quy)

Câu 3:
a: AB/AC=BD/CD=3/5
=>HB/HC=9/25
b: BC=BD+CD=36+60=96cm
HB/HC=9/25 nên 25HB-9HC=0 và HB+HC=96
=>HB=432/17cm; HC=1200/17cm
\(AH=\sqrt{\dfrac{432}{17}\cdot\dfrac{1200}{17}}=\dfrac{720}{17}\left(cm\right)\)
Bài 1:
AB/AC=2/3 nên HB/HC=4/9
=>HB=4/9HC
Ta có: \(AH^2=HB\cdot HC\)
=>\(HC^2\cdot\dfrac{4}{9}=36\)
=>HC=9(cm)
=>HB=4cm
BC=BH+CH=13cm
\(AB=\sqrt{4\cdot13}=2\sqrt{13}\left(cm\right)\)
\(AC=\sqrt{9\cdot13}=3\sqrt{13}\left(cm\right)\)


Đáp án D
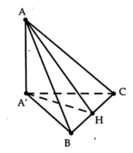
Ta có: B C ⊥ A A ' B C ⊥ A H
![]()
Do đó:
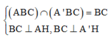
![]()
Mặt khác, tam giác A’BC vuông cân tại A’
nên A ' H = 1 2 B C = 3 a 2
Ta có:
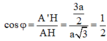
⇒ φ = 60 o

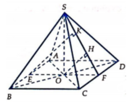
Tam giác ABC vuông cân tại A nên \(BC=2AH=2a\)
Từ đó \(S_{ABC}=\frac{1}{2}AH.BC=\frac{1}{2}a.2a=a^2\)
Vì \(SA\perp\left(ABC\right);AH\perp BC\) suy ra \(SH\perp BC\)
Do đó : \(\left(\left(SBC\right),\right)\left(ABC\right)=\widehat{SHA}=60^0\)
Suy ra \(SA=AH.\tan60^0=a\sqrt{3}\)
Vậy \(V_{SABC}=\frac{1}{3}SA.S_{ABC}=\frac{1}{3}a\sqrt{3}a^2=\frac{a^3\sqrt{3}}{3}\)

a: BC=10cm
b: Xét ΔABD có
AH là đường cao
AH là đường trung tuyến
Do đó: ΔABD cân tại A
hay AB=AD
c: Xét tứ giác ABED có
H là trung điểm của AE
H là trung điểm của BD
Do đó: ABED là hình bình hành
Suy ra: AB//ED
hay ED\(\perp\)AC
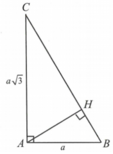
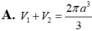


\(AH=\sqrt{AC^2-CH^2}=12\left(cm\right)\)
\(BH=\dfrac{AH^2}{CH}=\dfrac{12^2}{16}=9\left(cm\right)\)
CB=CH+BH=25(cm)
\(AB=\sqrt{9\cdot25}=15\left(cm\right)\)
Xét ΔABC vuông tại A có \(\sin C=\dfrac{AB}{BC}=\dfrac{3}{5}\)
nên \(\widehat{C}\simeq37^0\)