Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Nếu \(a>0\) thì hàm số \(y=ax^2+bx+c\)
Nghịch biến trên khoảng: \(\left(-\infty;-\dfrac{b}{2a}\right)\);
Đồng biến trên khoảng: \(\left(\dfrac{-b}{2a};+\infty\right)\).
Nếu \(a< 0\) thì hàm số \(y=ax^2+bx+c\):
Nghịch biến trên khoảng: \(\left(\dfrac{-b}{2a};+\infty\right)\);
Đồng biến trên khoảng: \(\left(-\infty;-\dfrac{b}{2a}\right)\).

- Khi a > 0, hàm số y = ax + b đồng biến trên khoảng (-∞; +∞) hay đồng biến trên R.
- Khi a < 0, hàm số y = ax + b nghịch biến trên khoảng (-∞; +∞) hay nghịch biến trên R.

Hàm số \(y=-f\left(x\right)\) đồng biến trên khoảng \(\left(a;b\right)\)

Xét hai số thực \(a;b\) bất kì thỏa mãn \(a>b>1\)
\(f\left(a\right)-f\left(b\right)=a+\frac{1}{a}-\left(b+\frac{1}{b}\right)=a-b+\frac{1}{a}-\frac{1}{b}\)
\(=a-b-\frac{a-b}{ab}=\left(a-b\right)\left(1-\frac{1}{ab}\right)\)
Do \(a>b>1\Rightarrow\left\{{}\begin{matrix}a-b>0\\ab>1\Rightarrow\frac{1}{ab}< 1\Rightarrow1-\frac{1}{ab}>0\end{matrix}\right.\)
\(\Rightarrow f\left(a\right)-f\left(b\right)>0\Rightarrow f\left(a\right)>f\left(b\right)\)
Vậy hàm đồng biến trên \(\left(1;+\infty\right)\)

Lấy x1;x2<1 sao cho x1<x2
\(A=\dfrac{f\left(x1\right)-f\left(x2\right)}{x_1-x_2}=\left(\dfrac{x_1-2}{x_1+1}-\dfrac{x_2-2}{x_2+1}\right):\left(x_1-x_2\right)\)
\(=\dfrac{x_1x_2+x_1-2x_2-2-x_1x_2-x_2+2x_1+2}{\left(x_1+1\right)\left(x_2+1\right)}\cdot\dfrac{1}{x_1-x_2}\)
\(=\dfrac{3x_1-3x_2}{\left(x_1+1\right)\left(x_2+1\right)}\cdot\dfrac{1}{x_1-x_2}=\dfrac{3}{\left(x_1+1\right)\left(x_2+1\right)}\)
x1<-1; x2<-1 nên x1+1<0; x2+1<0
=>(x1+1)(x2+1)>0
=>A>0
=>Hàm số đồng biến khi x<-1
Khi x1>-1; x2>-1 thì x1+1>0; x2+1>0
=>(x1+1)(x2+1)>0
=>A>0
=>Hàm số đồng biến khi x>-1
=>Hàm số đồng biến khi x<>-1

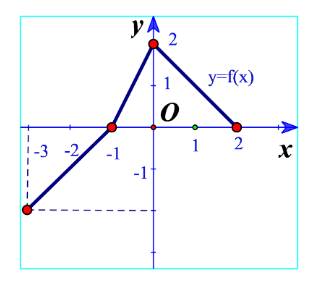
Từ đồ thị hàm số ta thấy khi x tăng từ -3 đến -1 và từ -1 đến 0 thì đồ thị đi lên nên hàm số đồng biến trên các khoảng (-3;-1) và (-1;0).
Khi x tăng từ 0 đến 2 thì đồ thị đi xuống nên hàm số nghịch biến trên (0;2).

Lời giải:
Lấy $x_1,x_2$ thuộc TXĐ của $f(x)$
Xét \(T=\frac{f(x_1)-f(x_2)}{x_1-x_2}=\frac{\frac{x_1-3}{x_1+5}-\frac{x_2-3}{x_2+5}}{x_1-x_2}\)
\(=\frac{8(x_1-x_2)}{(x_1+5)(x_2+5)(x_1-x_2)}=\frac{8}{(x_1+5)(x_2+5)}>0\) với mọi $x_1,x_2\in (-\infty; -5)$ và $x_1,x_2\in (-5;+\infty)$
Do đó hàm số đồng biến trên 2 khoảng đã cho.
Hàm số đồng biến trên (-∞,\(\dfrac{-b}{2a}\))
Hàm số nghịch biến trên (\(\dfrac{-b}{2a}\), +∞)
Hàm số đồng biến trên (\(\dfrac{-b}{2a}\), +∞)
Hàm số nghịch biến trên (-∞,\(\dfrac{-b}{2a}\))