Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Giả thiết: a//b
c cắt a và b tại A và B
Kết luận: \(\widehat{A_1}=\widehat{B_2}\)
Giả thiết:
Cho đường thẳng a,b,ca,b,c
Đường thẳng cc cắt đường thẳng a,ba,b lần lượt tại A,BA,B
ˆA1=ˆB1A1^=B1^
Kết luận:
ˆA2=ˆB1A2^=B1
Chứng minh:
Ta có: ˆA1=ˆB1A1^=B1^ (giải thiết)
Mà ˆA1=ˆA2A1^=A2^ (đối đỉnh)
⇒ˆA2=ˆB1(=ˆA1)⇒A2^=B1^(=A1^)
Mà ˆA2A2^ và ˆB1B1^ ở vị trí so le tron
⇒⇒ đpcm.
gt |1 đt cắt 2 đt //
-------------------------------------------
kl |tạo ra 2 cặp góc slt = nhau
a)
Giả thiết: Một đường thẳng cắt hai đường thẳng sao cho có một cặp góc so le trong bằng nhau.
Kết luận: Hai đường thẳng đó song song.
b) Giả thiết: Một đường thẳng cắt hai đường thẳng song song.
Kết luận: Hai góc so le trong bằng nhau.
a) Giả thiết: Một đường thẳng cắt hai đường thẳng sao cho có một cặp góc so le trong bằng nhau.
Kết luận: Hai đường thẳng đó song song.
b) Giả thiết: Một đường thẳng cắt hai đường thẳng song song.
Kết luận: Hai góc so le trong bằng nhau.
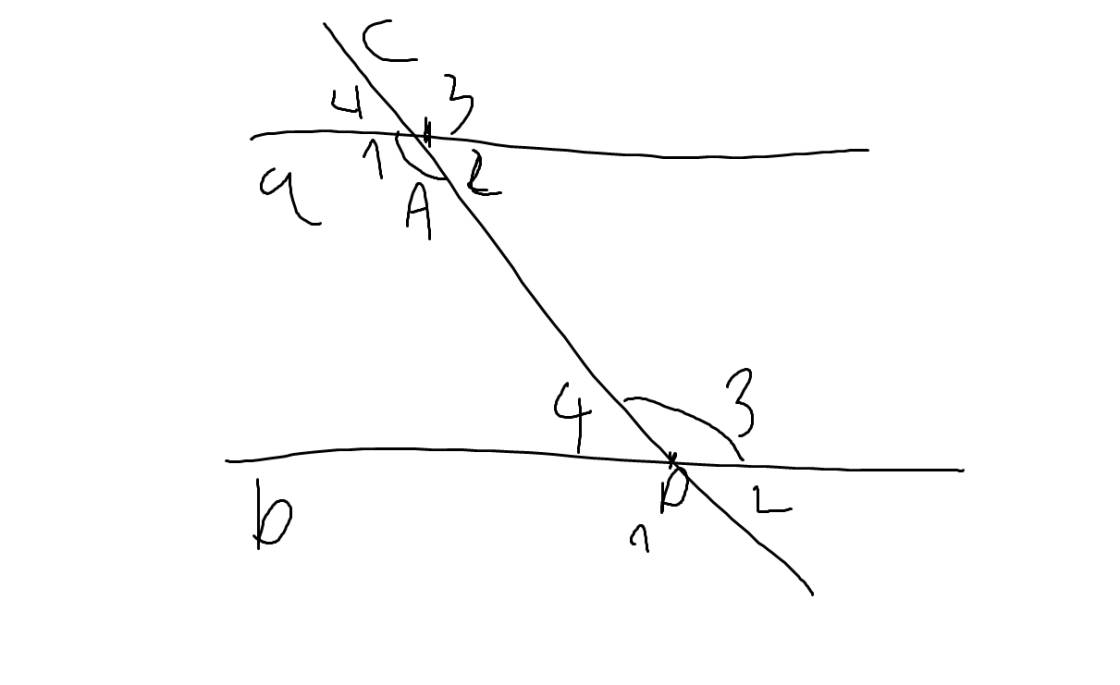
| GT | a cắt c tại A, a cắt b tại D \(\widehat{A_1}=\widehat{D_3}\) |
| KL | \(\widehat{D_3}+\widehat{A_2}=180^0\) |
\(\widehat{A_1}=\widehat{D_3}\)(hai góc so le trong bằng nhau)
mà \(\widehat{A_1}+\widehat{A_2}=180^0\)
nên \(\widehat{A_2}+\widehat{D_3}=180^0\)(ĐPCM)
a.
Giả thiêt : nếu 1 dường thẳng cắt hai dường thẳng sao cho co 1 cặp góc sole trong bằng nhau
Kết luận: thì 2 đường thẳng song song
b.
GT:nếu 1 đường thẳng cắt hai đường thẳng song song
KL: thì các góc sole trong bằng nhau
ko cần ****
Giả thiết: Đường thẳng cắt hai đường thẳng sao cho có một góc so le trong bằng nhau.
Kết luận: Hai đường thẳng đó song song.
GT: 1 đt cắt 2 đường thẳng...sole trong=nhau
Kl:2đt đó //
b)Gt:1đt cắt 2 đt//
Kl:2 góc sole trong=nhau