Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Em không nêu ra yêu cầu và các điều kiện liên quan của đề bài thì làm sao mn giúp em được?

Đề ví dụTimf x không âm biết căn (x-1)=...... Đề bải x không âm thì chỉ cần x>=0 thôi chứ ạ. Chỉ rõ chio mình hiểu nhá
Vì khi lấy ĐKXĐ thì lấy cả biểu thức trong căn mới đúng

Thì ĐKXĐ là phải lấy tất cả các biểu thức trong căn phải không âm
Bạn nhớ rằng $\sqrt{a}$ xác định khi mà $a\geq 0$, hay $a$ không âm.
Cho $a=x-1$ thì để $\sqrt{x-1}$ xác định thì $x-1\geq 0$
$\Leftrightarrow x\geq 1$

Bài 1:
** Nếu chị nhớ không nhầm thì dạng bài như thế này đến lớp 11 em mới được học mà??? Tuy nhiên, nếu em quan tâm thì chị có thể giải đáp sơ qua như sau:
Việc chọn thứ tự các số để xét nó là linh hoạt và không cố định. Tùy thuộc vào tính chất bài toán mà ta có cách chọn riêng.
Thông thường, việc chọn sẽ bắt nguồn từ những chữ số có tính chất đặc biệt (liên quan đến bài nhất), sau đó mới xét đến những cái sau. Cái nào càng bớt quan trọng thì càng xét sau.
Đi vào bài toán 1 chả hạn, vì sao phải xét d trước? Vì đề nó cho yêu cầu số lẻ, nên ta phải quan tâm đến cái đặc biệt là số cuối
Tiếp theo vì sao nên xét a? Vì a có tính chất đặc biệt thứ hai, a chỉ có thể nhận các giá trị khác 0
Cuối cùng mới đến những số b,c (không có gì đặc biệt)
-------------------------
Bài nam, nữ: Đề bài hỏi có bao nhiêu cách chọn 1 bạn nữ, 1 bạn nam thì em hiểu đơn giản là: có 18 bạn nữ nên có 18 cách chọn bạn nữ (đương nhiên). Nam cũng vậy.
"Cứ 1 bạn nữ lại có 1 cách chọn bạn nam"??? Cứ 1 bạn nữ ta lại có 15 cách chọn bạn nam chứ?
Giả sử em chọn ra bạn nữ U1 chả hạn, thì để ghép với U1 em có thể có 15 cách chọn bạn nam là A1, A2,...,A15
Bài 2:
Ý em hiểu đúng rồi. 5 bạn chơi cả cầu lông và bóng đá này nằm cả trong nhóm chơi cầu lông và bóng đá.
Ví dụ:
A là nhóm chơi cầu lông
B là nhóm chơi bóng đá
Nhóm A có thể bao gồm người chỉ chơi cầu lông và chơi cả 2 loại cầu lông, bóng đá. Nhóm B cũng vậy.
Khi nói em nằm trong trong top 5 bạn chơi cả cầu lông và bóng đá, thì bản thân em chơi cả trong nhóm 10 bạn cầu lông lẫn 15 bạn bóng đá.
Nói tóm gọn lại, 5 bạn này đồng thời cùng thuộc cả 2 nhóm cầu lông, bóng đá.

Tại sao không giải ra $\sqrt{P}$ và $\sqrt{P}$?
Em đã có $P$ rồi, nhưng với $\sqrt{P}$, em làm sao rút gọn được khi mà $P$ đã khá gọn rồi. Cũng chẳng có giá trị nào của $x$ để tính cụ thể $P, \sqrt{P}$ rồi đi so sánh. Vì vậy cách này không khả thi.
Vậy thì phải tìm hướng khác. Muốn so sánh 2 số, ta xét hiệu hai số đó.
$P-\sqrt{P}=\sqrt{P}(\sqrt{P}-1)$
Rõ ràng $\sqrt{P}$ đã dương rồi, giờ ta phải xem xét xem $\sqrt{P}-1$ âm hay dương, hay $P$ có lớn hơn 1 không
Đó là lý do vì sao bài giải như trên.
Còn câu hỏi khi nào giải ra từng cái $P$ và $\sqrt{P}$, thì đó là khi đề cho $x=2$ chả hạn, so sánh $P$ và $\sqrt{P}$.
Nhưg hầu như sẽ chẳng có đề nào ra kiểu vậy, mà đa số lợi dụng tính chất của phân thức đó để so sánh (ví dụ như trong bài tính chất nổi bật là $P>1$) cho nhanh. Đó là cái hay của đề bài.

Phân tích rõ một chút nhé :
- Căn bậc 2 của số x (bắt buộc là số x phải >=0 ) là \(\sqrt{x},-\sqrt{x}\)
Thì căn bậc 2 số học của x là \(\sqrt{x}\)(do\(\sqrt{x}\ge0\))
- Đối với trường hợp căn bậc 2 số học của x2 thì là |x|

Bạn chỉ cần hiểu là căn bậc hai số học của là một số x sao cho \(x^2=a\) và \(x\ge0\) thôi
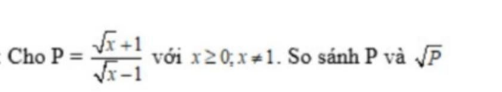
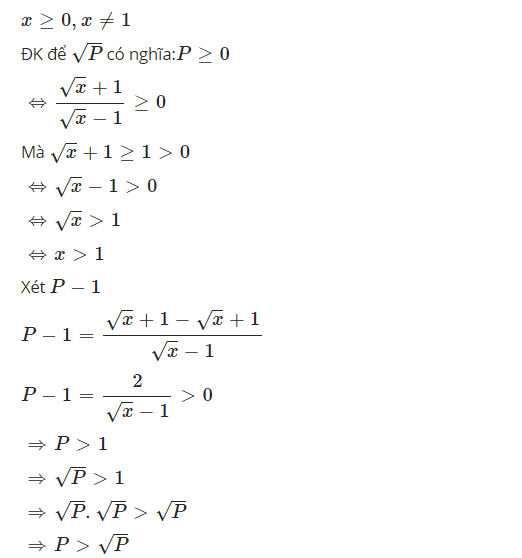
Nếu mẫu là \(\left(x+3\right)\left(x-3\right)\) thì điều kiện xác định sẽ là:
\(\left\{{}\begin{matrix}x+3\ne0\\x-3\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ne-3\\x\ne3\end{matrix}\right.\)
- Lưu ý là cả \(x+3\) và \(x-3\) đều phải khác 0
Bạn ơi có phải giống bằng 0 ạ