K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
18 tháng 7 2021
VD5:
\(A\cap B\ne\varnothing\Leftrightarrow2m-1\le m+3\)
\(\Leftrightarrow m\le4\)
VD6:
\(A\cap B\ne\varnothing\Leftrightarrow9a>\dfrac{4}{a}\)
\(\Leftrightarrow\dfrac{9a^2-4}{a}>0\)
\(\Leftrightarrow9a^2-4< 0\) (do \(a< 0\))
\(\Rightarrow-\dfrac{2}{3}< a< \dfrac{2}{3}\)
\(\Rightarrow-\dfrac{2}{3}< a< 0\)
VD6:
\(A\cap B=A\Leftrightarrow A\subset B\)
\(\Leftrightarrow\left\{{}\begin{matrix}-1\ge m\\3\le m+5\end{matrix}\right.\) \(\Rightarrow-2\le m\le-1\)
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 4 2021
1.
\(\dfrac{1-cosx+cos2x}{sin2x-sinx}=\dfrac{1-cosx+2cos^2x-1}{2sinx.cosx-sinx}\)
\(=\dfrac{cosx\left(2cosx-1\right)}{sinx\left(2cosx-1\right)}=\dfrac{cosx}{sinx}=cotx\)
2.
\(\dfrac{1+tan^4x}{tan^2x+cot^2x}=\dfrac{1+tan^4x}{tan^2x+\dfrac{1}{tan^2x}}=\dfrac{1+tan^4x}{\dfrac{tan^4x+1}{tan^2x}}=tan^2x\)
3.
\(sin^4x+cos^4x=sin^4x+cos^4x+2sin^2x.cos^2x-2sin^2x.cos^2x\)
\(=\left(sin^2x+cos^2x\right)^2-2sin^2x.cos^2x\)
\(=1-2sin^2x.cos^2x\)
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 4 2021
4.
Áp dụng câu 3:
\(sin^4x+cos^4x=1-2sin^2x.cos^2x\)
\(=1-\dfrac{1}{2}\left(2sinx.cosx\right)^2\)
\(=1-\dfrac{1}{2}sin^22x\)
5.
\(sin\left(x+y\right)sin\left(x-y\right)=\dfrac{1}{2}cos\left[\left(x-y\right)-\left(x+y\right)\right]-\dfrac{1}{2}cos\left[\left(x-y\right)+\left(x+y\right)\right]\)
\(=\dfrac{1}{2}\left(cos2y-cos2x\right)=\dfrac{1}{2}\left(1-2sin^2y\right)-\dfrac{1}{2}\left(1-2sin^2x\right)\)
\(=sin^2x-sin^2y\)
6.
\(tanx+cotx=\dfrac{sinx}{cosx}+\dfrac{cosx}{sinx}=\dfrac{sin^2x+cos^2x}{sinx.cosx}\)
\(=\dfrac{1}{sinx.cosx}=\dfrac{2}{2sinx.cosx}=\dfrac{2}{sin2x}\)
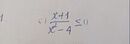
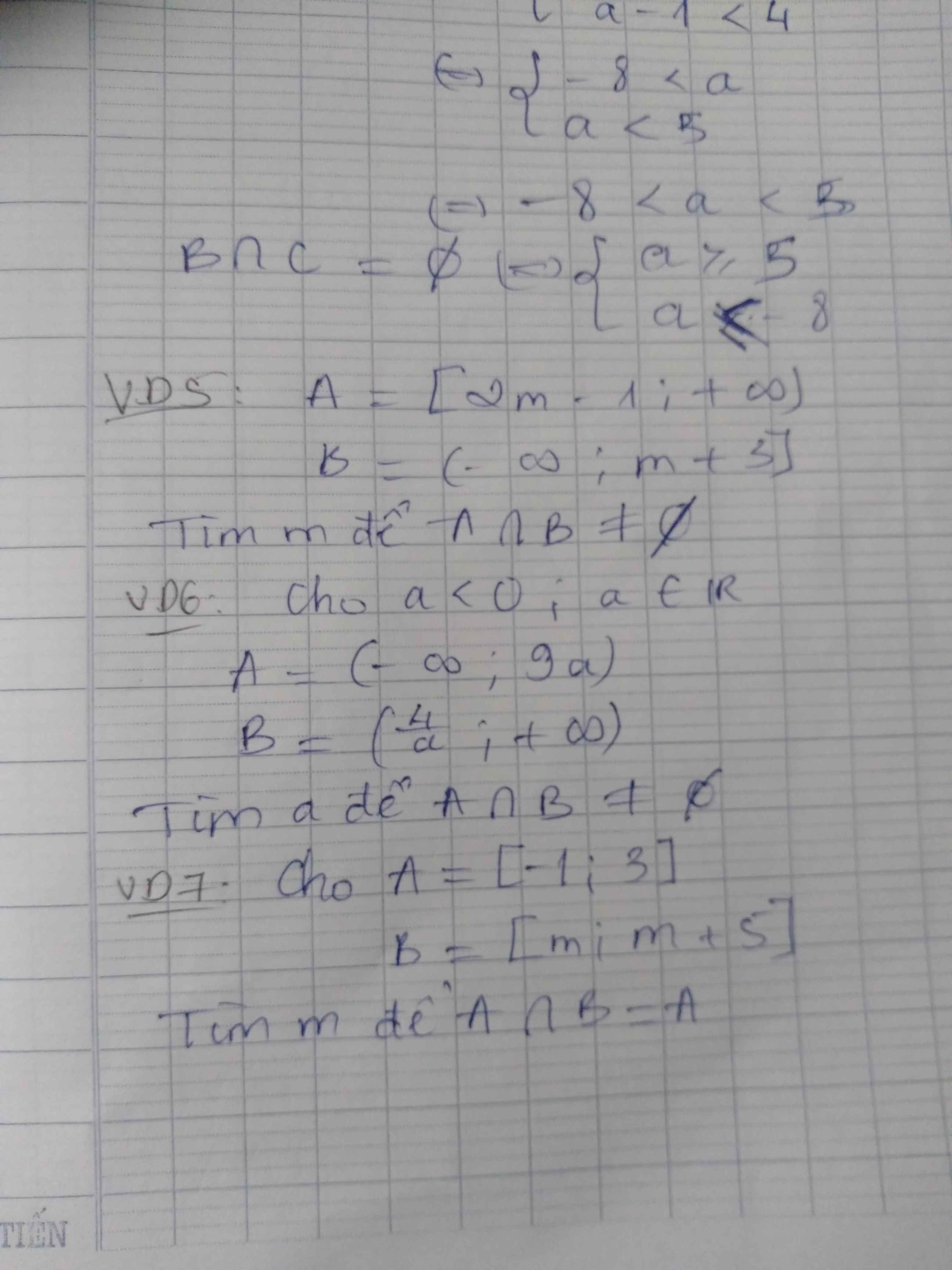
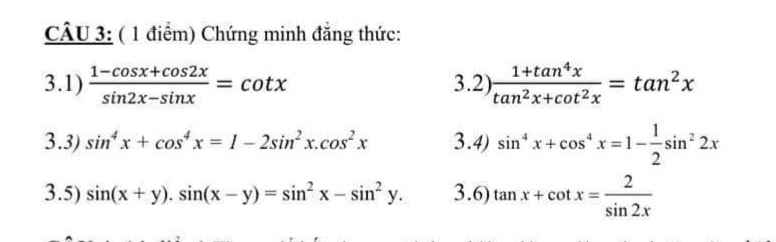
bạn vẽ trục số ra thì ra đc
\(-1\le x\le2\)
kết luận.......
bổ sung :
\(ĐKXĐ:x\ne2\)
\(< =>-1\le x< 2\)