Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Olm chào em, cảm ơn đánh giá của em về chất lượng bài giảng của Olm, cảm ơn em đã đồng hành cùng Olm trên hành trình tri thức. Chúc em học tập hiệu quả và vui vẻ cùng Olm em nhé!

\(3x^2-5x+2\)
\(=3x^2-3x-2x+2\)
\(=3x\left(x-1\right)-2\left(x-1\right)\)
\(=\left(x-1\right)\left(3x-2\right)\)
Đề sai rồi bạn phải + 2 chứ

Ta có
\(\hept{\begin{cases}x+y-xy=55\\x^2+y^2=325\end{cases}}\Leftrightarrow\hept{\begin{cases}2\left(x+y\right)-2xy=110\\\left(x+y\right)^2-2xy=325\end{cases}}\)
Lấy dưới trừ trên vế theo vế ta được
(x + y)2 - 2(x + y) = 215
\(\Leftrightarrow\orbr{\begin{cases}x+y=1+6\sqrt{6}\\x+y=1-6\sqrt{6}\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}xy=6\sqrt{6}-54\\xy=-6\sqrt{6}-54\end{cases}}\)
Ta lại có
Ta lại có
x3 - y3 = (x - y)(x2 + xy + y2) =
\(\sqrt{\left(x+y\right)^2-4xy}\left(x^2+xy+y^2\right)\)
Giờ chỉ việc thế số vô là có đáp án nhé

Olm chào em, cảm ơn đánh giá của em về chất lượng bài giảng của Olm, cảm ơn em đã đồng hành cùng Olm trên hành trình tri thức. Chúc em học tập hiệu quả và vui vẻ cùng Olm em nhé!

\(P=\dfrac{x^3+8y^3}{4^3+4^3}=\dfrac{\left(x+2y\right)^3-3\cdot x\cdot2y\cdot\left(x+2y\right)}{128}\)
\(=\dfrac{\left(-8\right)^3-6\cdot\left(-6\right)\cdot\left(-8\right)}{128}=\dfrac{128-6\cdot48}{128}=-\dfrac{5}{4}\)

Dung à mày (:
Ta có \(\frac{1}{\left(x+1\right)^2\left(x+2\right)}=\frac{a}{x+1}+\frac{b}{\left(x+1\right)^2}+\frac{c}{x+2}\)
\(\Leftrightarrow\frac{1}{\left(x+1\right)^2\left(x+2\right)}=\frac{a\left(x+1\right)\left(x+2\right)}{\left(x+1\right)^2\left(x+2\right)}+\frac{b\left(x+2\right)}{\left(x+1\right)^2\left(x+2\right)}+\frac{c\left(x+1\right)^2}{\left(x+1\right)^2\left(x+2\right)}\)
\(\Leftrightarrow\frac{1}{\left(x+1\right)^2\left(x+2\right)}=\frac{a\left(x^2+3x+2\right)}{\left(x+1\right)^2\left(x+2\right)}+\frac{bx+2b}{\left(x+1\right)^2\left(x+2\right)}+\frac{c\left(x^2+2x+1\right)}{\left(x+1\right)^2\left(x+2\right)}\)
\(\Leftrightarrow\frac{1}{\left(x+1\right)^2\left(x+2\right)}=\frac{ax^2+3ax+2a+bx+2b+cx^2+2cx+c}{\left(x+1\right)^2\left(x+2\right)}\)
\(\Leftrightarrow\frac{1}{\left(x+1\right)^2\left(x+2\right)}=\frac{x^2\left(a+c\right)+x\left(3a+b+2c\right)+\left(2a+2b+c\right)}{\left(x+1\right)^2\left(x+2\right)}\)
\(\Rightarrow1=x^2\left(a+c\right)+x\left(3a+b+2c\right)+\left(2a+2b+c\right)\)
Đồng nhất hệ số ta được :
\(\hept{\begin{cases}a+c=0\\3a+b+2c=0\\2a+2b+c=1\end{cases}}\)=> Chịu :)) Khó quá không làm được ... Hoặc do đề sai ;-;
Không sai == Trong sách Nâng cao và phát triển toán 8 tập 1 trang 33 bài 123 ý c
T cũng chịu '-'
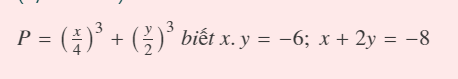
Olm chào em, cảm ơn đánh giá của em về chất lượng bài giảng của Olm, cảm ơn em đã đồng hành cùng Olm trên hành trình tri thức. Chúc em học tập hiệu quả và vui vẻ cùng Olm em nhé!