Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

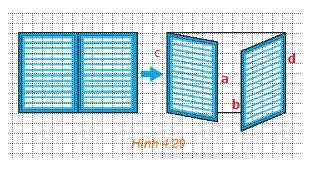
Vì a//c, b//d (do cánh cửa là hình chữ nhật)
Mà c//d.
Suy ra, a//b.
Do đó, hai mép ngoài của chúng luôn song song với nhau.
Nếu hai cánh cửa sổ có dạng hình thang như Hình 4.30, hai cánh cửa để hai mép ngoài của chúng song song với nhau khi cả hai cánh cửa được khép lại.

Để tính giá thành làm cầu thang, ta cần tính diện tích của từng bậc thang và sau đó cộng lại.
Diện tích của một bậc thang có thể tính bằng công thức: Diện tích = Chiều dài x Chiều rộng.
Ta có thể tính diện tích của từng bậc thang như sau:
Bậc đầu tiên: Diện tích = 189cm x 35cm = 6615cm² Bậc thứ hai: Diện tích = (189cm - 7cm) x 35cm = 6230cm² Bậc thứ ba: Diện tích = (189cm - 2*7cm) x 35cm = 5845cm² ... Bậc cuối cùng: Diện tích = 63cm x 35cm = 2205cm²
Sau đó, ta cộng lại diện tích của từng bậc thang để tính tổng diện tích cầu thang:
Tổng diện tích = 6615cm² + 6230cm² + 5845cm² + ... + 2205cm²
Để tính giá thành của cầu thang, ta nhân tổng diện tích cầu thang với giá thành một mét vuông:
Giá thành = Tổng diện tích x 1250000 đồng/m²
Vì không có thông tin cụ thể về số bậc thang trong câu hỏi, nên không thể tính được tổng diện tích và giá thành chính xác. Tuy nhiên, để xác định giá thành gần với số nào dưới đây, ta có thể ước lượng giá thành bằng cách lấy diện tích trung bình của các bậc thang và nhân với số bậc thang.
Giả sử số bậc thang là n, ta có:
Diện tích trung bình = (6615cm² + 6230cm² + 5845cm² + ... + 2205cm²) / n
Giá thành ước lượng = Diện tích trung bình x 1250000 đồng/m²

Vì các thanh chắn của chiếc thang song song với với nhau nên hình chiếu của chúng cũng song song với nhau.

a)
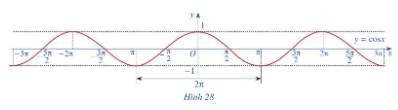
x | \( - \pi \) | \( - \frac{{2\pi }}{3}\) | \[ - \frac{\pi }{2}\] | \( - \frac{\pi }{3}\) | 0 | \(\frac{\pi }{3}\) | \(\frac{\pi }{2}\) | \(\frac{{2\pi }}{3}\) | \(\pi \) |
\(y = \cos x\) | -1 | \( - \frac{1}{2}\) | 0 | \(\frac{1}{2}\) | 1 | \(\frac{1}{2}\) | 0 | \( - \frac{1}{2}\) | -1
|
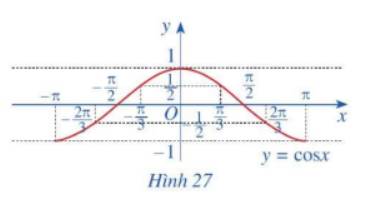
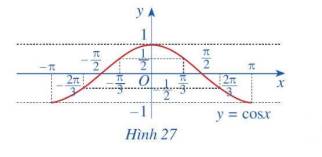
b) Trong mặt phẳng tọa độ Oxy, hãy biểu diễn các điểm (x; y) trong bảng giá trị ở câu a. Bằng cách làm tương tự, lấy nhiều điểm \(\left( {x;\cos x} \right)\) với \(x \in \left[ { - \pi ;\pi } \right]\) và nối lại ta được đồ thị hàm số \(y = \cos x\) trên đoạn \(x \in \left[ { - \pi ;\pi } \right]\) (Hình 27)
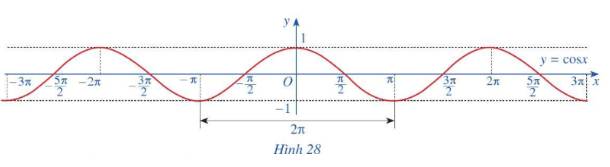
c) Làm tương tự như trên đối với các đoạn \(\left[ { - 3\pi ; - \pi } \right]\), \(\left[ {\pi ;3\pi } \right]\),...ta có đồ thị hàm số \(y = \cos x\)trên R được biểu diễn ở Hình 28.

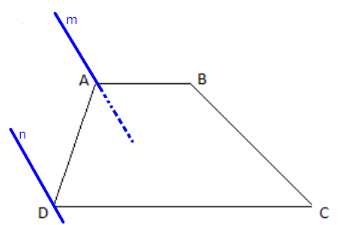
Ta có: m // n suy ra m // (C,n).
Có: AB // CD (do ABCD là hình thang) suy ra AB // (C,n).
Mặt phẳng (B,m) chứa hia đường thẳng cắt nhau m và AB song song với mp(C,n) suy ra (B,m) // (C,n).

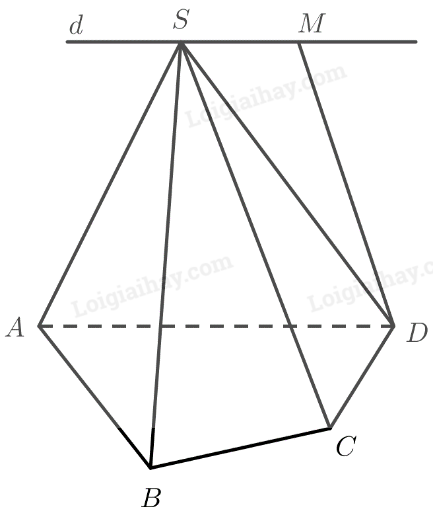
\(A{\rm{D}}M{\rm{S}}\) là hình thang có hai đáy là \(A{\rm{D}}\) và \(M{\rm{S}}\) nên \(A{\rm{D}}\parallel M{\rm{S}}\).
Theo đề bài ta lại có \(d\parallel A{\rm{D}}\).
Do đó \(d \equiv MS\) (theo định lí 1).
Lại có: \(SM \subset \left( {A{\rm{D}}M{\rm{S}}} \right) \Rightarrow d \subset \left( {A{\rm{D}}M{\rm{S}}} \right) \Rightarrow d \subset \left( {SA{\rm{D}}} \right)\).

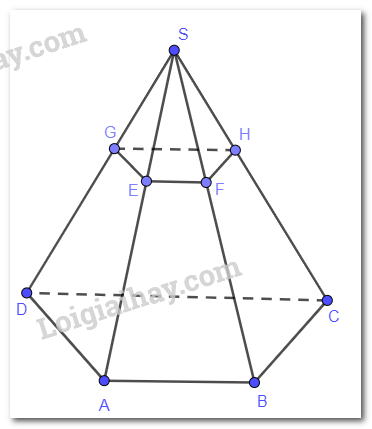
Mặt phẳng (SAD) chứa đường thẳng AD song song với mp(P) nên mặt phẳng (P) cắt (SAD) theo giao tuyến song song với AD. Vẽ EG // AD (G thuộc SD) thì EG là giao tuyến của (P) và (SAD).
Mặt phẳng (SAB) chứa đường thẳng AB song song với mp(P) nên mặt phẳng (P) cắt (SAB) theo giao tuyến song song với AB. Vẽ EF // AB (F thuộc SB) thì EF là giao tuyến của (P) và (SAB).
Ta có AB // CD, EF // AB suy ra CD // EF hay CD // mp(P)
Mặt phẳng (SCD) chứa đường thẳng CD song song với mp(P) nên mặt phẳng (P) cắt (SCD) theo giao tuyến song song với CD. Vẽ GH // CD (H thuộc SC) thì GH là giao tuyến của (P) và (SCD).
FH thuộc (P), FH thuộc (SBC) suy ra FH là giao tuyến của (P) và (SBC).
Tứ giác EFGH có EF // GH (vì cùng song song với CD) suy ra EFGH là hình thang.

\(ABCD\) là hình thang có đáy lớn \(AB \Rightarrow AB\parallel CD\).
Vì hình chiếu song song của hai đường thẳng song song là hai đường thẳng song song hoặc trùng nhau, mà hình chiếu song song của \(ABCD\) là tứ giác \(A'B'C'D'\) nên \(A'B'\parallel C'D'\). Vậy \(A'B'C'D'\) cũng là một hình thang.
Vì phép chiếu song song không làm thay đổi tỉ số độ dài của hai đoạn thẳng nằm trên hai đường thẳng song song hoặc trùng nhau, mà \(AB = 2CD,AB\parallel CD\) và \(A'B'\parallel C'D'\) nên \(A'B' = 2C'D'\).




Các mặt của bậc thang đều song song với mặt sàn nên chúng đôi một song song với nhau.
Mặt phẳng tường cắt các mặt bậc thang tại các mép nằm trên bờ tường nên chúng song song với nhau.