K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
12 tháng 11 2021
\(x=x_0+v_0t+\dfrac{1}{2}at^2\)
Ta có: \(x_0=2m;v_0=4\)m/s;\(a=10m\)/s2
Phương trình chuyển động:
\(x=x_0+v_0t+\dfrac{1}{2}at^2\)\(=2+4t+\dfrac{1}{2}\cdot10t^2=2+4t+5t^2\)
Chọn A.
NP
1
AM
5 tháng 4 2023
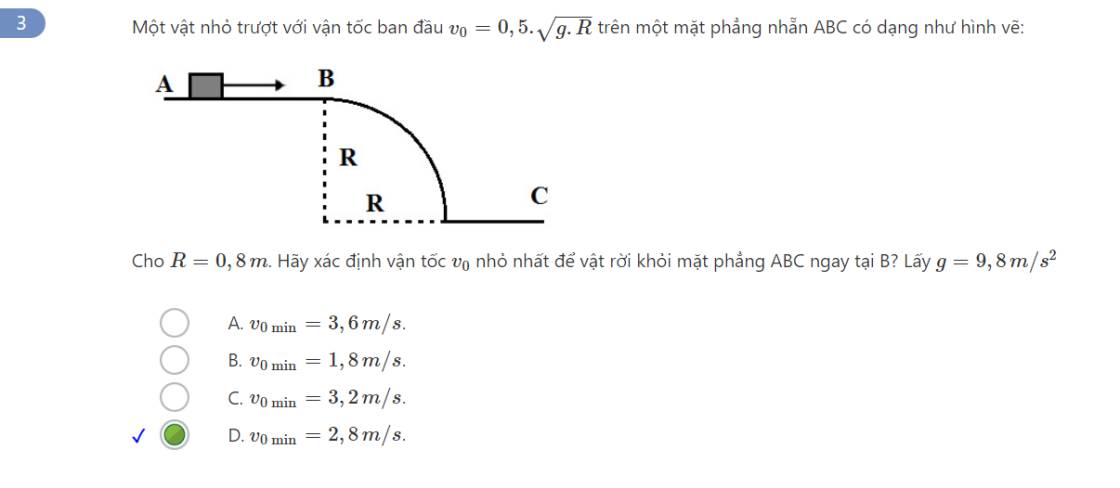
Phân tích lực tại vị trí B, theo định luật II Newton ta có:
\(\overrightarrow{P}+\overrightarrow{N}=m\overrightarrow{a}\) (*)
Chiếu (*) lên trục Oy chiều dương hướng lên và vuông góc với phương chuyển động, ta có:
\(N-P=-ma_{ht}\)
Để vật rời khỏi mặt phẳng ABC ngay tại B thì \(N=0,P\le ma_{ht}\)
\(\Rightarrow P\le ma_{ht}\) \(\Leftrightarrow mg\le ma_{ht}\Leftrightarrow g\le\dfrac{v_0^2}{R}\Rightarrow v_0\ge\sqrt{gR}=2,8\)
Vậy \(v_{0min}=2,8\) (m/s)
20 tháng 8 2016
Chọn gốc tọa độ tại nơi vật bắt đầu xuất phát, mốc thời gian từ lúc vật bắt đầu chuyển động, chiều dương là chiều chuyển động.
(Thời gian đi 3/4 quãng đường cuối = thời gian đi cả quãng đường - thời gian đi 1/4 quãng đường đầu)
Ta có:
- Cả quãng đường đi với thời gian là t (giây):
\(s=v_0t+\frac{1}{2}at^2=\frac{1}{2}at^2\) (*)
\(\frac{1}{4}s=v_0t'+\frac{1}{2}a\left(t'\right)^2=\frac{1}{2}a\left(t'\right)^2\) (**)
(Vì v(0) = 0)
Lấy (*) chia (**) \(\frac{t^2}{\left(t'\right)^2}=4\Rightarrow t'=\frac{1}{2}t\)
Thời gian đi 3/4 quãng đường cuối là:
\(t''=t-t'=t-\frac{1}{2}t=\frac{1}{2}t\)
HD
Hà Đức Thọ
Admin
20 tháng 8 2016
+ Thời gian đi đoạn đường S là 6s.
+ Tìm thời gian đi 1/4 đoạn đường S ban đầu là t1
+ Từ đó suy ra thời gian đi 3/4 đoạn đường sau là: t2 = 6 - t1
Chọn D.
Vì chuyển động thẳng đều là chuyển động chỉ theo một đường thẳng.
Đúng ạ