
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) \(x^2+2x+1-y^2\)
\(=\left(x+1\right)^2-y^2\)
\(=\left(x+1+y\right)\left(x+1-y\right)\)
b) \(25x^2+1-9y^2-10x\)
\(=25x^2-10x+1-9y^2\)
\(=\left(5x-1\right)^2-9y^2\)
\(=\left(5x-1+3y\right)\left(5x-1-3y\right)\)
c) \(x^2-1+4y-4y^2\)
\(=x^2-\left(1-4y+4y^2\right)\)
\(=x^2-\left(1-2y\right)^2\)
\(=\left(x+1-2y\right)\left(x-1+2y\right)\)


a: Xét ΔABC có
M là trung điểm của AC
H là trung điểm của bC
Do đó: MH là đường trung bình của ΔABC
Suy ra: MH//AB
hay ABHM là hình thang


\(45.\)
\(M=a^3+b^3+3ab\left(a^2+b^2\right)+6a^2b^2\left(a+b\right)\)
\(=\left(a+b\right)\left(a^2-ab+b^2\right)+3ab\left[\left(a^2+2ab+b^2\right)-2ab\right]+6a^2b^2\left(a+b\right)\)
\(=\left(a+b\right)\left(a^2-ab+b^2\right)+3ab\left[\left(a+b\right)^2-2ab\right]+6a^2b^2\left(a+b\right)\)
\(=a^2-ab+b^2+3ab\left(1-2ab\right)+6a^2b^2\)
\(=a^2-ab+b^2+3ab-6a^2b^2+6a^2b^2\)
\(=a^2+2ab+b^2\)
\(=\left(a+b\right)^2\)
\(=1^2\)
\(=1\).
42:
a^3+b^3+c^3-3abc
=(a+b)^3+c^3-3ab(a+b)-3bac
=(a+b+c)(a^2+2ab+b^2-ac-bc+c^2)-3ab(a+b+c)
=0
=>a^3+b^3+c^3=3abc
44:
a: x^3+y^3+3xy
=(x+y)^3-3xy(x+y)+3xy
=1^3-3xy+3xy=1
b: x^3-y^3-3xy
=(x-y)^3+3xy(x-y)-3xy
=1^3+3xy-3xy=1

Bài 1:
\(VT=1\cdot\left(a+b\right)\left(a^2+b^2\right)\left(a^4+b^4\right)\left(a^8+b^8\right)\left(a^{16}+b^{16}\right)\)
\(=\left(a-b\right)\left(a+b\right)\left(a^2+b^2\right)\cdot\left(a^4+b^4\right)\left(a^8+b^8\right)\left(a^{16}+b^{16}\right)\)
\(=\left(a^2-b^2\right)\left(a^2+b^2\right)\left(a^4+b^4\right)\left(a^8+b^8\right)\left(a^{16}+b^{16}\right)\)
\(=\left(a^4-b^4\right)\left(a^4+b^4\right)\left(a^8+b^8\right)\left(a^{16}+b^{16}\right)\)
\(=a^{32}-b^{32}\)

k bt đó là thật k nx nhưng tạm tin nha nhưng bù lại văn mk chỉ đc 8 điểm thôi
 câu nào cx đc ah
câu nào cx đc ah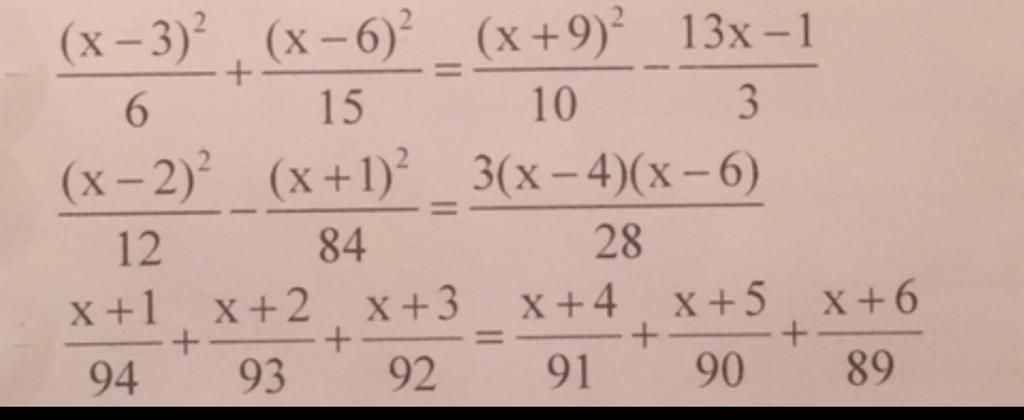
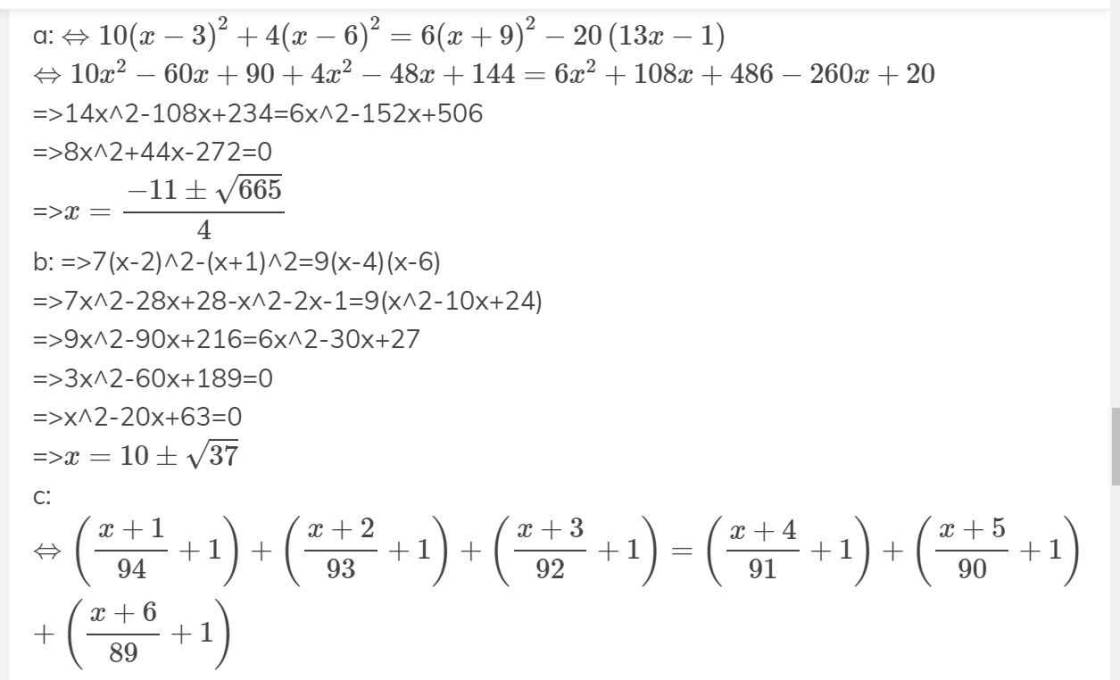
 Nhanh giúp em vs ạ.Mỗi người vài câu cx đc
Nhanh giúp em vs ạ.Mỗi người vài câu cx đc
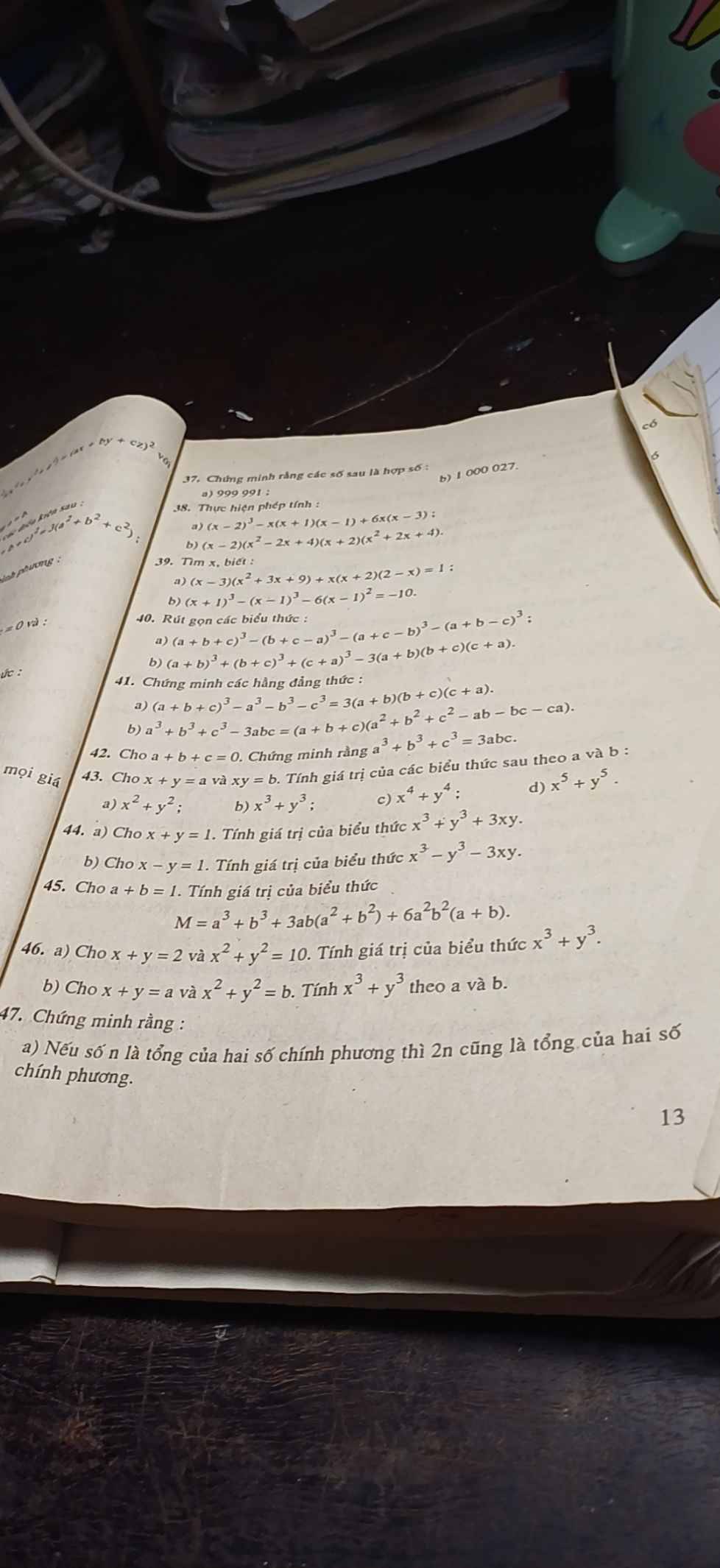
`3x^2 -8x+4`
`=3x^2-2x-6x+4`
`=x(3x-2) - 2(3x-2)`
`=(3x-2)(x-2)`
__
`4x^2-4x-3`
`=4x^2 +2x-6x-3`
`=2x(2x+1) - 3(2x+1)`
`=(2x+1)(2x-3)`
__
`x^2-6x+5`
`=x^2-x-5x+5`
`=x(x-1)-5(x-1)`
`=(x-1)(x-5)`
__
`x^4 +2x^2-3`
`=x^4+x^3+3x^2+3x-x^3-x^2-3x-3`
`=x(x^3+x^2+3x+3)-1(x^3+x^2+3x+3)`
`=(x^3+x^2+3x+3) (x-1)`
`=[x^2(x+1) +3(x+1)](x-1)`
`= (x^2+3)(x+1)(x-1)`
__
`x^4+64`
`=x^4+16x^2+64-16x^2`
`=(x^2)^2 +16x^2 +8^2 -(4x)^2`
`=(x^2 +8)^2 -(4x)^2`
`= (x^2+8-4x)(x^2 +8+4x)`