
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Ta có: \(A=x^2+3x+3\)
\(=x^2+2\cdot x\cdot\dfrac{3}{2}+\dfrac{9}{4}+\dfrac{3}{4}\)
\(=\left(x+\dfrac{3}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\forall x\)
Dấu '=' xảy ra khi \(x=-\dfrac{3}{2}\)
b) Ta có: \(B=x^2+4x+9\)
\(=x^2+4x+4+5\)
\(=\left(x+2\right)^2+5\ge5\forall x\)
Dấu '=' xảy ra khi x=-2
c) Ta có: \(C=-x^2+x+1\)
\(=-\left(x^2-x-1\right)\)
\(=-\left(x^2-2\cdot x\cdot\dfrac{1}{2}+\dfrac{1}{4}-\dfrac{5}{4}\right)\)
\(=-\left(x-\dfrac{1}{2}\right)^2+\dfrac{5}{4}\le\dfrac{5}{4}\forall x\)
Dấu '=' xảy ra khi \(x=\dfrac{1}{2}\)
d)Ta có: \(D=-4x^2+4x+1\)
\(=-\left(4x^2-4x-1\right)\)
\(=-\left(4x^2-4x+1-2\right)\)
\(=-\left(2x-1\right)^2+2\le2\forall x\)
Dấu '=' xảy ra khi \(x=\dfrac{1}{2}\)
e) Ta có: \(E=\dfrac{1}{16}x^2-9x+10\)
\(=\left(\dfrac{1}{4}x\right)^2-2\cdot\dfrac{1}{4}x\cdot18+324-314\)
\(=\left(\dfrac{1}{4}x-18\right)^2-314\ge-314\forall x\)
Dấu '=' xảy ra khi \(\dfrac{1}{4}x-18=0\)
hay x=72
f) Ta có: \(F=4x^4+12x^2+11\)
\(\Leftrightarrow F\ge11\forall x\)
Dấu '=' xảy ra khi x=0

9:
a: -x^3+3x^2-3x+1
=(-x)^3+3*(-x)^2*1+3*(-x)*1^2+1^3
=(-x+1)^3
b: z^3-z^2+1/3z-1/27
=z^3-3*z^2*1/3+3*z*(1/3)^2-(1/3)^3
=(z-1/3)^3
c: x^6-3x^4y+3x^2y^2-y^3
=(x^2)^3-3*(x^2)^2*y+3*x^2*y^2-y^3
=(x^2-y)^3
d: =(x-y)^3+3*(x-y)^2*1/3+3*(x-y)*(1/3)^2+(1/3)^3
=(x-y+1/3)^3
Ví dụ 9:
a) \(-x^3+3x^2-3x+1\)
\(=-\left(x^3-3x^2+3x-1\right)\)
\(=-\left(x-1\right)^3\)
b) \(x^3-x^2+\dfrac{1}{3}x-\dfrac{1}{27}\)
\(=x^3-3\cdot\dfrac{1}{3}\cdot x^2+3\cdot\left(\dfrac{1}{3}\right)^2\cdot x-\left(\dfrac{1}{3}\right)^3\)
\(=\left(x-\dfrac{1}{3}\right)^3\)
c) \(x^6-3x^4y+3x^2y^2-y^3\)
\(=\left(x^2\right)^3-3\cdot\left(x^2\right)^2\cdot y+3\cdot x^2\cdot y^2-y^3\)
\(=\left(x^2-y\right)^3\)
d) \(\left(x-y\right)^3+\left(x-y\right)^2+\dfrac{1}{3}\left(x-y\right)+\dfrac{1}{27}\)
\(=\left(x-y\right)^3+3\cdot\dfrac{1}{3}\cdot\left(x-y\right)^2+3\cdot\left(\dfrac{1}{3}\right)^2\cdot\left(x-y\right)+\left(\dfrac{1}{3}\right)^3\)
\(=\left(x-y+\dfrac{1}{3}\right)^3\)

e) Ta có: \(x^3-4x-14x\left(x-2\right)=0\)
\(\Leftrightarrow x\left(x-2\right)\left(x+2\right)-14x\left(x-2\right)=0\)
\(\Leftrightarrow x\left(x-2\right)\left(x+2-14\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=2\\x=12\end{matrix}\right.\)
e)x3-4x+14x(x-2)=0
⇔ x(x2-4)+14x(x-2)=0
⇔ x(x-2)(x+2)+14x(x-2)=0
⇔ (x-2)(x2+2x+14x)=0
⇔ x(x-2)(x+16)=0
\(\Leftrightarrow\left\{{}\begin{matrix}x=0\\x-2=0\\x+16=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\x=2\\x=-16\end{matrix}\right.\)
g)x2(x+1)-x(x+1)+x(x-1)=0
⇔ (x+1)(x2-x)+x(x-1)=0
⇔ x(x+1)(x-1)+x(x-1)=0
⇔ x(x-1)(x+2)=0
\(\Leftrightarrow\left\{{}\begin{matrix}x=0\\x-1=0\\x+2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\x=1\\x=-2\end{matrix}\right.\)

a) A=(n+1)(n+2)(n+3)(n+4)+1
A= (n+1)(n+4)(n+2)(n+3)+1
A=(n2+5n+4)(n2+5n+6)+1
Đặt n2+5n+5 =y ta có:
A=(y-1)(y+1) +1 =y2-1+1=y2
\(\Rightarrow\)A= (n2+5n+5) là 1 số chính phương
b)Đề sai ở chỗ 2017.2018 sửa lại là: 2.2017.2018
Thì A = 20172+20182+2.2017.2018
A = (2017+2018)2
A = 40352 là 1 số chính phương .

Câu 1 :
(x2 + 7x + 10) : (x+2) = x+5
Câu 2 :
a\ x2 - 9 + y2 - 2xy
= (x2 - 2xy + y2) - 9
= (x - y)2 - 9
= (x - y - 3)(x - y + 3)
b\ 10x + x2 + 21
= x2 + 3x + 7x + 21
= x(x + 3) + 7(x + 3)
= (x + 3)(x + 7)
Bài 3 :
a\ \(\frac{x^2}{x^2+1}-\frac{2x}{x^2+1}+\frac{1}{x^2+1}\)
= \(\frac{x^2-2x+1}{x^2+1}\)
= \(\frac{ \left(x+1\right)^2}{x^2+1}\)
b\




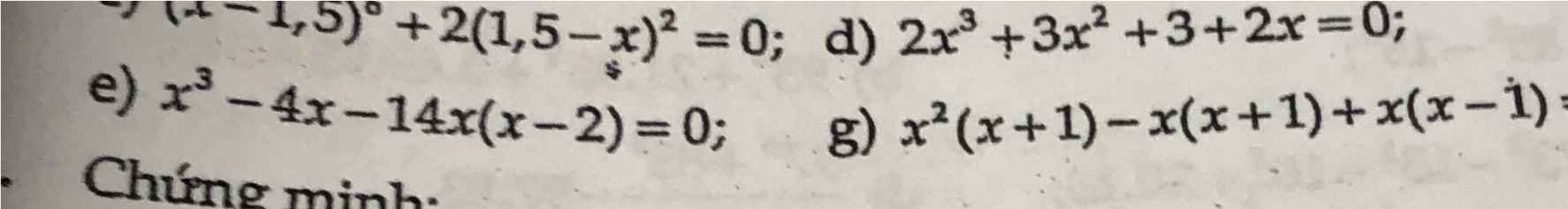
Nhầm ^4 nha
\(\left(a^2+ab+b^2\right)\left(a^2-ab+b^2\right)-\left(a^4+b^4\right)\)
\(=\left[\left(a^2+b^2\right)^2-a^2b^2\right]-\left(a^4+b^4\right)\)
\(=a^4+b^4+2a^2b^2-a^2b^2-a^4-b^4\)
\(=a^2b^2\)