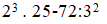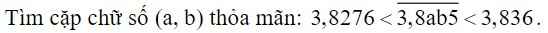K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
DT
2
19 tháng 8 2016
9/2-1/2-1+3x=1/2+1/3
=)8/2-1+3x=5/6
=)3+3x=5/6
=)3x=5/6-3
=)3x=13/6
x=13/18
19 tháng 8 2016
ta có: 9/2 - 1/2 - (1-3x)=1/2 + 1/3
<=>9/2 - 1/2 - (1-3x)=5/6
<=>1/2 - (1-3x) =9/2-5/6
<=>1/2 - (1-3x) =11/3
<=> 1 - 3x = 19/6
<=> 3x =13/6
<=> x =13/18
31 tháng 10 2020
\(3^{x+2}+3^x=10\)
\(3^x\cdot\left(3^2+1\right)=10\)
\(3^x\cdot\left(9+1\right)=10\)
\(3^x\cdot10=10\)
\(3^x=10:10\)
\(3^x=1\)
\(3^x=3^0\)
\(\Rightarrow x=0\)
Cho tớ hỏi là câu này chọn C đúng kh ạ :"))?
KV
23 tháng 10 2023
3n + 4 = 3n - 6 + 10
= 3(n - 2) + 10
Để (3n + 4) ⋮ (n - 2) thì 10 ⋮ (n - 2)
⇒ n - 2 ∈ Ư(10) = {-10; -5; -2; -1; 1; 2; 5; 10}
⇒ n ∈ {-8; -3; 0; 1; 3; 4; 7; 12}
Mà n là số tự nhiên
⇒ n ∈ {0; 1; 3; 4; 7; 12}
3 tháng 2
\(3,8276< \overline{3,8ab5}< 3,836\)
=>\(276< \overline{ab5}< 360\)
=>\(\left(a,b\right)\in\left\{\left(2;8\right);\left(2;9\right);\left(3;0\right);\left(3;1\right);\left(3;2\right);\left(3;3\right);\left(3;4\right);\left(3;5\right)\right\}\)
18 tháng 7 2023
\(A=2+2^2+2^3+...+2^{260}\)
\(A=2\left(1+2\right)+2^2\left(1+2\right)+2^3\left(1+2\right)+...+2^{259}\left(1+2\right)\)
\(A=2.3+2^2.3+2^3.3+...+2^{259}.3\)
\(A=3\left(2+2^2+2^3+...+2^{259}\right)⋮3\left(1\right)\)
\(A=\left(2+2^2+2^3\right)+...+\left(2^{258}+2^{259}+2^{260}\right)\)
\(A=2.\left(1+2+2^2\right)+...+2^{258}.\left(1+2+2^2\right)\)
\(A=2.7+...+2^{258}.7\Rightarrow A=7\left(2+...+2^{258}\right)⋮7\left(2\right)\)
\(A=\left(2+2^2+2^3+2^4\right)+...+\left(2^{257}+2^{258}+2^{259}+2^{260}\right)\)
\(A=2.\left(1+2+2^2+2^3\right)+...+2^{257}.\left(1+2+2^2+2^3\right)\)
\(A=2.15+...+2^{257}.15\Rightarrow A=15\left(2+...+2^{257}\right)⋮5\left(15⋮5\right)\left(3\right)\)
\(\left(1\right),\left(2\right),\left(3\right)\Rightarrow dpcm\)
