Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

df,jtiofqegnjkjhrwjrths/shgdhldgfjydhd,.jykhtlghkfsj ;lsjks;rthjak k;dkyjtkrfmnhglkkjtgkfsyhtrkerkyjhsgjhfksrkh
do hieu day

a) \(3^{x + 1} = 81\)
\(3^{x + 1} = 3^{4}\)
x + 1 = 4
x = 3
Vậy ..............
b) \(3^{x}.9^{2}= 729\)
\(3^{x}= 729 : 81 = 9\)
\(3^{x}= 3^{2}\)
=> x = 2
Vậy ................
c) \((x^{2})^{3}= 4096\)
\(x^{6}= 4096\)
\(x^{6}= 4^{6}\)
=> x = 4
Vậy ................

\(H=\int\limits^3_2\frac{1}{x^2\left(x+1\right)}dx\)
Sử dụng hệ số bất định để tách biểu thức tích phân:
\(\frac{1}{x^2\left(x+1\right)}=\frac{A}{x}+\frac{B}{x^2}+\frac{C}{x+1}=\frac{Ax\left(x+1\right)+B\left(x+1\right)+Cx^2}{x^2\left(x+1\right)}=\frac{\left(A+C\right)x^2+\left(A+B\right)x+B}{x^2\left(x+1\right)}\)
Đồng nhất 2 vế ta được: \(\left\{{}\begin{matrix}A+C=0\\A+B=0\\B=1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}A=-1\\B=C=1\end{matrix}\right.\)
\(\Rightarrow H=\int\limits^3_2\left(-\frac{1}{x}+\frac{1}{x^2}+\frac{1}{x+1}\right)dx=\left(-lnx-\frac{1}{x}+ln\left(x+1\right)\right)|^3_2=3ln2-2ln3+\frac{1}{6}\)

đã hỏi thầy giáo và đã hiêu câu này. Quả thực đáp án A là đúng
Cảm ơn ai đang đã quan tâm đến.

Sửa đề : \(x^4-6x^2+8x-3=(x-1)^3(x+3)\)
Lời giải:
Ta thấy tổng các hệ số của đa thức bằng $0$ nên đa thức có nghiệm là $1$, nghĩa là khi phân tích sẽ có thừa số $x-1$ và cứ thế triển khai thôi:
\(x^4-6x^2+8x-3=(x^4-x^2)-(5x^2-5x)+(3x-3)\)
\(=x^2(x^2-1)-5x(x-1)+3(x-1)\)
\(=(x-1)[x^2(x+1)-5x+3]\)
\(=(x-1)(x^3+x^2-5x+3)\)
\(=(x-1)[x^3-x^2+2x^2-2x-(3x-3)]\)
\(=(x-1)[x^2(x-1)+2x(x-1)-3(x-1)]\)
\(=(x-1)(x^2+2x-3)(x-1)=(x-1)^2(x^2-x+3x-3)\)
\(=(x-1)^2[x(x-1)+3(x-1)]=(x-1)^2(x-1)(x+3)=(x-1)^3(x+3)\)

đáp án là :
Hàm số đã cho xác định trên D=R.
Tính y' = -3x2 + 12x - 9. Cho y' = 0 ⇔ -3x2 + 12x - 9 = 0 ⇔
Bảng biến thiên:
Dựa vào bảng biến thiên,hàm số đồng biến trên (1;3).
Hàm số nghịch biến trên các khoảng (-∞; 1) và (3; +∞)
Hàm số đã cho xác định trên D=R.
Tính y' = -3x2 + 12x - 9. Cho y' = 0 ⇔ -3x2 + 12x - 9 = 0 ⇔
Bảng biến thiên:
Dựa vào bảng biến thiên,hàm số đồng biến trên (1;3).
Hàm số nghịch biến trên các khoảng (-∞; 1) và (3; +∞)
P/S : quá dễ , t là thần đồng mà .
Mỗi ngày 3 T i c k , giờ làm như lời hứa đi
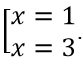
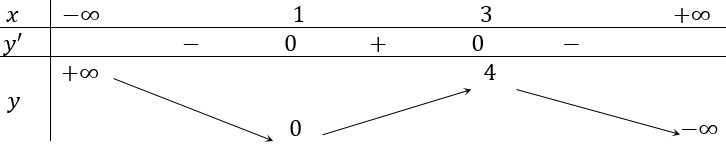
TRONG 3 NGÀY SAU ĐÓ TIẾT LỘ ĐÁP ÁN
NẾU KÔ TRẢ LỜI ĐƯỢC THÌ ĐƯA TÔI 5 COIN