câu a và b nhé
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TL
1
7 tháng 9 2016
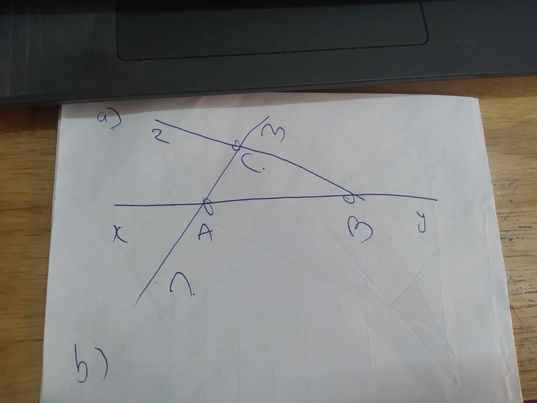
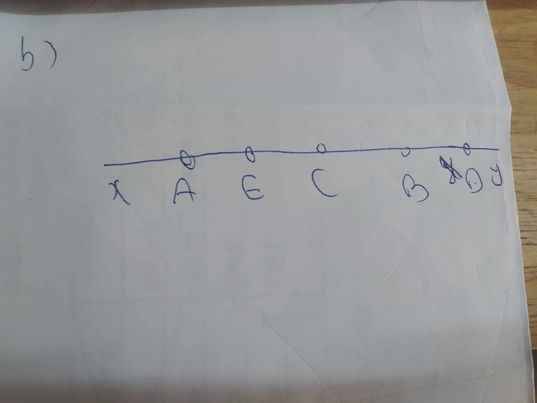
bạn ơi bạn có chắc ko?Đầu tiên mình cũng làm như bạn đó nhưng mà đọc kĩ lại có chi tiết B NẰM GIỮA N VÀ A nha, nhưng trong hình bạn vẽ điểm B nằm giữa điểm M và N mà
Hay là cái đó là vẽ từng phần một, mình cg ko hiểu đề bài lắm nên mới lên đây hỏi nè
TN
23 tháng 4 2018
giả sử tìm được hai chữ số a và b sao cho: \(\frac{a}{b}=a,b\left(b\in N^∗\right)\)
Rõ ràng: \(\frac{a}{b}=a.\frac{1}{b}\)
Mà \(\frac{1}{b}\le1\Rightarrow a.\frac{1}{b}\le a\) hay \(\frac{a}{b}\le a\left(2\right)\)
Từ (1) và (2) \(\Rightarrow\frac{a}{b}< a,b\) nên không tìm đc số a và b điều kiện thỏa mãn đề bài
Tích nha
Học tốt
10 tháng 9 2020
A=4 ; B=7
Vì A={3,4,6,8} B={4,6,7,8}
A có 3 nhưng B ko có 3
B có 7 nhưng A ko có 7
mà A={3,4,6,8} nên b=7
B={(a-1);4;6;7;8} nên A phải =4
ta có A={3,4,7,6,8
B={3,4,6,7,8}
10 tháng 9 2020
Các phần tử không (chưa) chung của A và B là: 3,b của A và (a-1),7 của B
A=B khi và chỉ khi các phần tử đó trùng nhau hay \(\orbr{\begin{cases}3=a-1,b=7\Rightarrow a=4,b=7\\7=a-1,b=3\Rightarrow a=8,b=3\end{cases}}\)
2 tháng 4 2017
\(2A=1+\frac{2}{2}+\frac{3}{2^2}+...+\frac{2016}{2^{2015}}\)
\(2A-A=1+\frac{1}{2}+\frac{1}{2^2}+...+\frac{1}{2^{2015}}-\frac{2016}{2^{2016}}\)
\(A=1+\frac{1}{2}+\frac{1}{2^2}+...+\frac{1}{2^{2015}}-\frac{1}{2^{2016}}< 1+\frac{1}{2}+\frac{1}{2^2}+...+\frac{1}{2^{2015}}\)(1)
Ta có
\(1+\frac{1}{2}+\frac{1}{2^2}+...+\frac{1}{2^{2015}}=1+\left(1-\frac{1}{2}+\frac{1}{2}-\frac{1}{2^2}+...+\frac{1}{2^{2014}}-\frac{1}{2^{2015}}\right)=1+\left(1-\frac{1}{2^{2015}}\right)\)
\(< 1+1=2\)(2)
Từ (1) và (2) ta có A<2
Vậy A<B
2 tháng 4 2017
A=\(\frac{1}{2}+\frac{2}{2^2}+\frac{3}{2^3}+.........+\frac{2016}{2^{2016}}\\ 2A=1+\frac{2}{2}+\frac{3}{2^2}+........+\frac{2016}{2^{2015}}\\ 2A-A=\left(\frac{2}{2}-\frac{1}{2}\right)+\left(\frac{3}{2^2}-\frac{2}{2^2}\right)+\left(\frac{4}{2^3}-\frac{3}{2^3}\right)+.........\left(\frac{2016}{2^{2015}}-\frac{2015}{2^{2015}}\right)+\left(1-\frac{2016}{2^{2015}}\right)\\ A=\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+.....+\frac{1}{2^{2015}}+\left(1-\frac{2016}{2^{2015}}\right)\)
\(GọiC=\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+.....+\frac{1}{2^{2015}}\\ 2C=1+\frac{1}{2}+\frac{1}{2^3}+......+\frac{1}{2^{2014}}\\ 2C-C=C=1-\frac{1}{2^{2015}}\)
Thay C vào A , ta có : A = 1 - 1/2^2015 + 1 - 1/2^2016 =2 - 1/2^2015 - 1/2^2016<2 =B->A<B