
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
góc B chung
=>ΔABC đồng dạng với ΔHBA
=>AB/HB=BC/BC=AC/HA
=>AB*AH=AC*HB
b: AH=căn 5^2-3^2=4cm
BI là phân giác
=>IH/HB=IA/AB
=>IH/3=IA/5=(IH+IA)/(3+5)=4/8=1/2
=>IH=1,5cm; IA=2,5cm

1: Sửa đề: Qua N kẻ đường song song với PC cắt AB tại F
Xét tứ giác CNFP có NF//PC
nên CNFP là hình thang

1
Với \(\left\{{}\begin{matrix}x\ne2\\x\ne-1\\x\ne\sqrt{\dfrac{1}{2}}\end{matrix}\right.\)
\(M=\left(\dfrac{x-1}{2-x}-\dfrac{x^2}{x^2-x-2}\right)\left(\dfrac{x^2+2x+1}{4x^4-4x^2+1}\right)\\ =\left(\dfrac{\left(x-1\right)\left(x+1\right)}{\left(2-x\right)\left(x+1\right)}+\dfrac{x^2}{\left(x+1\right)\left(2-x\right)}\right)\left(\dfrac{\left(x+1\right)^2}{\left(2x^2-1\right)^2}\right)\\ =\dfrac{x^2-1+x^2}{\left(x+1\right)\left(2-x\right)}\left(\dfrac{\left(x+1\right)^2}{\left(2x^2-1\right)^2}\right)\\ =\dfrac{\left(2x^2-1\right)\left(x+1\right)^2}{\left(x+1\right)\left(2-x\right)\left(2x^2-1\right)^2}\\ =\dfrac{x+1}{\left(2-x\right)\left(2x^2-1\right)}\)
2
Để M = 0 thì \(\dfrac{x+1}{\left(2-x\right)\left(2x^2-1\right)}=0\Rightarrow x+1=0\Rightarrow x=-1\) (loại)
Vậy không có giá trị x thỏa mãn M = 0
1) \(M=\left(\dfrac{x-1}{2-x}-\dfrac{x^2}{x^2-x-2}\right)\cdot\dfrac{x^2+2x+1}{4x^4-4x^2+1}\) (ĐK: \(\left\{{}\begin{matrix}x\ne2\\x\ne-1\\x\ne\sqrt{\dfrac{1}{2}}\end{matrix}\right.\))
\(M=\left(\dfrac{-\left(x-1\right)}{x-2}-\dfrac{x^2}{\left(x-2\right)\left(x+1\right)}\right)\cdot\dfrac{\left(x+1\right)^2}{\left(2x^2-1\right)^2}\)
\(M=\left(\dfrac{-\left(x-1\right)\left(x+1\right)}{\left(x-2\right)\left(x+1\right)}-\dfrac{x^2}{\left(x-2\right)\left(x+1\right)}\right)\cdot\dfrac{\left(x+1\right)^2}{\left(2x^2-1\right)^2}\)
\(M=\left(\dfrac{-\left(x^2-1\right)-x^2}{\left(x-2\right)\left(x+1\right)}\right)\cdot\dfrac{\left(x+1\right)^2}{\left(2x^2-1\right)^2}\)
\(M=\left(\dfrac{-x^2+1-x^2}{\left(x-2\right)\left(x+1\right)}\right)\cdot\dfrac{\left(x+1\right)^2}{\left(2x^2-1\right)^2}\)
\(M=\dfrac{-2x^2+1}{\left(x-2\right)\left(x+1\right)}\cdot\dfrac{\left(x+1\right)^2}{\left(2x^2-1\right)^2}\)
\(M=\dfrac{-\left(2x^2-1\right)\left(x+1\right)^2}{\left(x-2\right)\left(x+1\right)\left(2x^2-1\right)^2}\)
\(M=\dfrac{-\left(x+1\right)}{\left(x-2\right)\left(2x^2-1\right)}\)
2) Ta có: \(M=0\)
\(\Rightarrow\dfrac{-\left(x+1\right)}{\left(x-2\right)\left(2x^2-1\right)}=0\)
\(\Leftrightarrow-\left(x+1\right)=0\)
\(\Leftrightarrow-x=1\)
\(\Leftrightarrow x=-1\left(ktm\right)\)

a, Mẫu khác 0 <=> x ≠ 1 thì phân thức xác định.
b, Khi x = 1000 và x =1 giá trị lần lượt là: 999 và ko xác định vì x phải khác 1


a: =x^2+6x+9+x^2-6x+9+2x^2-32
=4x^2-14
b: =(x+3-10+x)^2=(2x-7)^2=4x^2-28x+49
c: =(x-3-x+5)^2=2^2=4
e: =x^2+10x+25-x^2+10x-25=20x
d: A=(5-1)(5+1)(5^2+1)(5^4+1)/4
=(5^2-1)(5^2+1)(5^4+1)/4
=(5^4-1)(5^4+1)/4
=(5^8-1)/4
g: =x^2-9-x^2-4x+5
=-4x-4



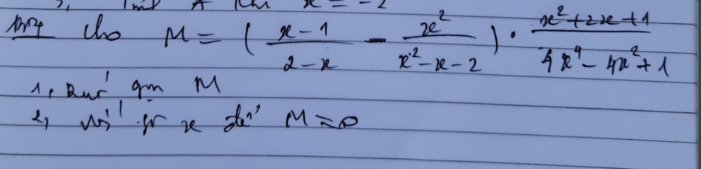
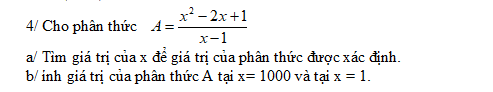
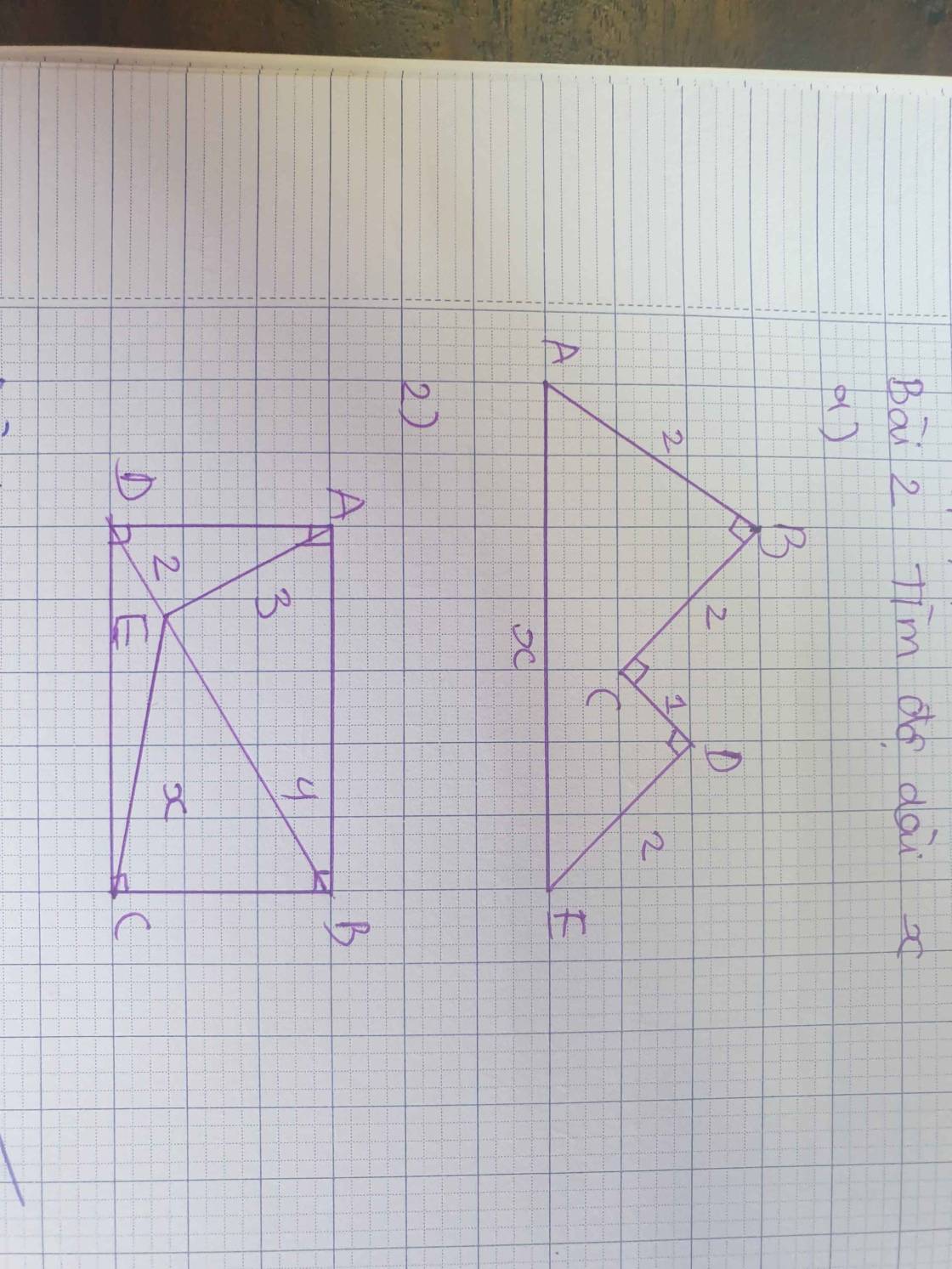 MN giúp mik giải với ạ
MN giúp mik giải với ạ mn giúp mik bài này với ạ này là hằng đẳng thúc ạ(ảnh hơi mờ mn thông cảm)
mn giúp mik bài này với ạ này là hằng đẳng thúc ạ(ảnh hơi mờ mn thông cảm)
Đặt x^2 = a, y^2 = b, z^2 = c => abc = (xyz)^2 = 1
\(A=\frac{a}{b+c-a}+\frac{b}{c+a-b}+\frac{c}{a+b-c}\)
\(=\frac{a\left(c+a-b\right)\left(a+b-c\right)+b\left(a+b-c\right)\left(b+c-a\right)+c\left(b+c-a\right)\left(c+a-b\right)}{\left(b+c-a\right)\left(c+a-b\right)\left(a+b-c\right)}\)
Ta có: \(a\left(c+a-b\right)\left(a+b-c\right)=a\left[a^2-\left(b-c\right)^2\right]=a^3-ab^2-c^2a+2abc\)
Tương tự: \(b\left(a+b-c\right)\left(b+c-a\right)=b^3-bc^2-a^2b+2abc\)
\(c\left(b+c-a\right)\left(c+a-b\right)=c^3-ca^2-b^2c+2abc\)
Tử thức của A = \(a^3+b^3+c^3-a^2b-ab^2-b^2c-bc^2-c^2a-ca^2+6abc\)
Lại có: \(\left(b+c-a\right)\left(c+a-b\right)\left(a+b-c\right)=\left(b+c-a\right)\left[a^2-b^2-c^2+2bc\right]\)
\(=-a^3-b^3-c^3+a^2b+ab^2+b^2c+bc^2+c^2a+ca^2-2abc\)
\(\Rightarrow A=\frac{a^3+b^3+c^3-a^2b-ab^2-b^2c-bc^2-c^2a-ca^2+6abc}{-a^3-b^3-c^3+a^2b+ab^2+b^2c+bc^2+c^2a+ca^2-2abc}\)
\(=\frac{4abc}{-a^3-b^3-c^3+a^2b+ab^2+b^2c+bc^2+c^2a+ca^2-2abc}-1\)
\(=\frac{4}{\left(b+c-a\right)\left(c+a-b\right)\left(a+b-c\right)}-1\)
\(=\frac{4}{\left(y^2+z^2-x^2\right)\left(z^2+x^2-y^2\right)\left(x^2+y^2-z^2\right)}-1\)