K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
4 tháng 12 2021
Bài 2:
\(a,P=8ab^2+7ab^2=15ab^2\\ Q=\dfrac{3}{2}a^2b-\dfrac{5}{8}a^2b-\dfrac{7}{8}a^2b=0\)
Vì \(ab^2\ne0\Rightarrow\) P không đồng dạng với Q
b, ảnh nhỏ quá ko nhìn thấy
4 tháng 12 2021
Bài 2:
b: \(A=-8mn+\dfrac{1}{5}mn=-\dfrac{39}{5}mn\)
\(B=4mn-\dfrac{3}{2}mn=\dfrac{5}{2}mn\)
Do đó: A đồng dạng với B
26 tháng 12 2021
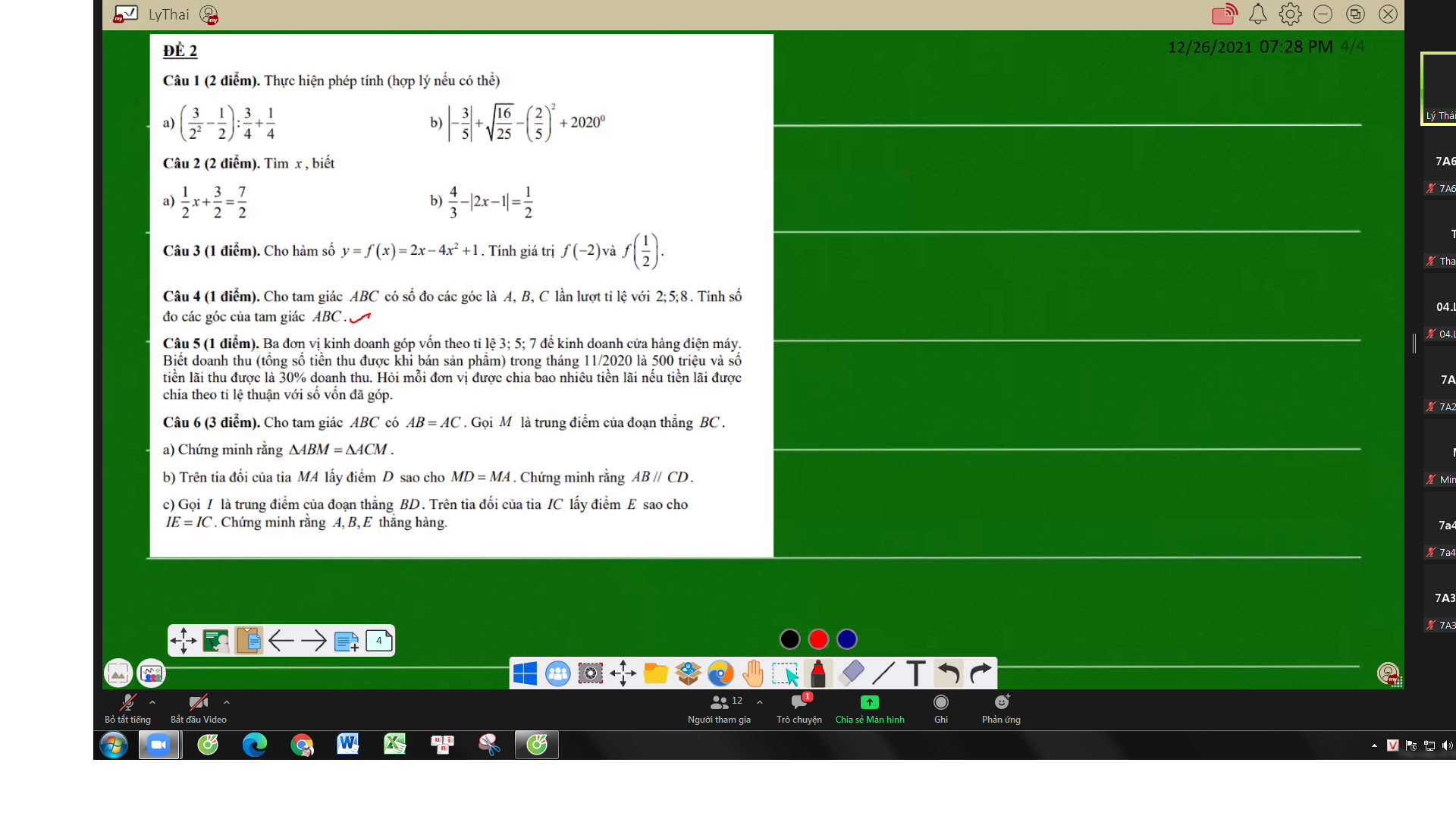
Câu 4:
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{2}=\dfrac{b}{5}=\dfrac{c}{8}=\dfrac{a+b+c}{2+5+8}=\dfrac{180}{15}=12\)
Do đó: a=24; b=60; c=96
3 tháng 1 2022
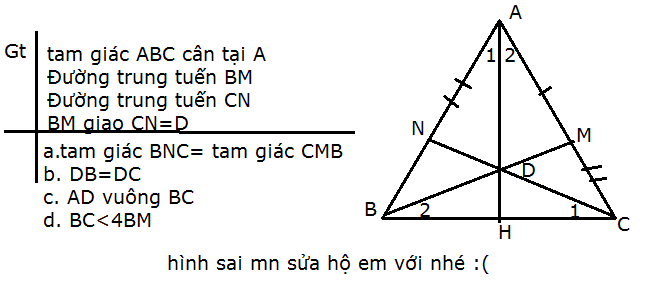
a: Xét ΔANB và ΔANC có
AN chung
NB=NC
AB=AC
Do đó: ΔANB=ΔANC
b: Ta có: ΔANB=ΔANC
nên \(\widehat{ANB}=\widehat{ANC}\)
Ta có: ΔABC cân tại A
mà AN là đường trung tuyến
nên AN là đường cao
25 tháng 1 2022
Theo Pytago tam giác ABC vuông tại A
BC^2 = AB^2 + AC^2
25 = 9 + 16 * luôn đúng *
làm giúp mình câu 1 thôi nha CẢm ơn nhìuuuu
Bài 8: \(sin\widehat{B}=\dfrac{AC}{BC}\) \(\Rightarrow\) \(\dfrac{AC}{BC}=sin30^o=\dfrac{1}{2}\) \(\Rightarrow\) BC=2AC.