
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


`3)(x+4)/(x-3)-(x-3)/(x+4)=(x^2+18x+7)/(x^2+x-12)`
`đk:x ne 3,x ne -4`
Nhân 2 vế với `(x-3)(x+4) ne 0` ta có:
`(x+4)^2-(x-3)^2=x^2+18x+7`
`<=>x^2+8x+16-x^2+6x-9=x^2+18x+7`
`<=>14x+7=x^2+18x+7`
`<=>x^2+4x=0`
`<=>x(x+4)=0`
Vì `x ne -4=>x+4 ne 0`
`<=>x=0`
Vậy `S={0}`

Dạng này thì đặt k là chắc ăn nhất !
Đặt \(\frac{a}{b}=\frac{c}{d}=k\)
\(\Rightarrow a=bk;c=dk\)
Ta có:
\(\frac{7a^2+5ac}{7a^2-5ac}=\frac{7b^2k^2+5bk\cdot dk}{7b^2k^2-5bk\cdot dk}=\frac{7b^2k^2+5bdk^2}{7b^2k^2-5bdk^2}=\frac{bk^2\left(7b+5d\right)}{bk^2\left(7b-5d\right)}=\frac{7b+5d}{7b-5d}\)
\(\frac{7b^2+5bd}{7b^2-5bd}=\frac{b\left(7b+5d\right)}{b\left(7b-5d\right)}=\frac{7b+5d}{7b-5d}\)
\(\Rightarrowđpcm\)
Đặt \(\frac{a}{b}=\frac{b}{d}=k\)
Vì\(\frac{a}{b}=k\Rightarrow a=bk\)
Vì\(\frac{b}{d}=k\Rightarrow b=dk\)
Ta có:
\(\frac{7a^2+5ac}{7a^2-5ac}=\frac{7\left(bk\right)^2+5.bk.dk}{7\left(bk\right)^2-5.bk.dk}=\frac{7b^2.k^2+5bd.k^2}{7b^2.k^2-5bd.k^2}=\frac{k^2.\left(7b^2+5bd\right)}{k^2.\left(7b^2-5bd\right)}\)
\(=\frac{7b^2+5bd}{7b^2-5bd}\)
\(\Rightarrowđpcm\)

3: \(\left(3x+5\right)\left(2x-7\right)\)
\(=6x^2-21x+10x-35\)
\(=6x^2-11x-35\)
4: \(\left(5x-2\right)\left(3x+4\right)\)
\(=15x^2+20x-6x-8\)
\(=15x^2+14x-8\)

Bài 2:
Ta có: \(3n^3+10n^2-5⋮3n+1\)
\(\Leftrightarrow3n^3+n^2+9n^2+3n-3n-1-4⋮3n+1\)
\(\Leftrightarrow3n+1\in\left\{1;-1;2;-2;4;-4\right\}\)
\(\Leftrightarrow3n\in\left\{0;-3;3\right\}\)
hay \(n\in\left\{0;-1;1\right\}\)


\(\dfrac{x^3-27}{x^2-9}\left(x\ne\pm3\right)\)
\(=\dfrac{x^3-3^3}{x^2-3^2}\)
\(=\dfrac{\left(x-3\right)\left(x^2+3x+9\right)}{\left(x-3\right)\left(x+3\right)}\)
\(=\dfrac{x^2+3x+9}{x+3}\)


 4 ấy
4 ấy


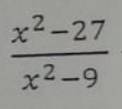

7b. \(k\left(x\right)=2x\left(4x+1\right)-8x^2\left(x+1\right)+\left(2x\right)^3-2x+3\)
\(=8x^2+2x-8x^3-8x^2+8x^3-2x+3\)
\(k\left(x\right)=3\)
Vậy: Ta có đpcm
Bài 7:
b: Ta có: \(K\left(x\right)=2x\left(4x+1\right)-8x^2\left(x+1\right)+\left(2x\right)^3-2x+3\)
\(=8x^2+2x-8x^3-8x^2+8x^3-2x+3\)
=3