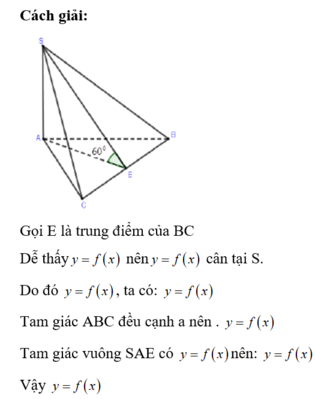
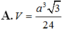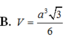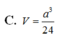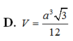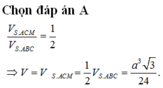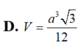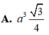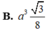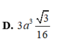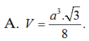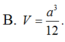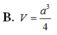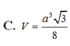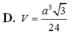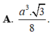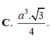Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

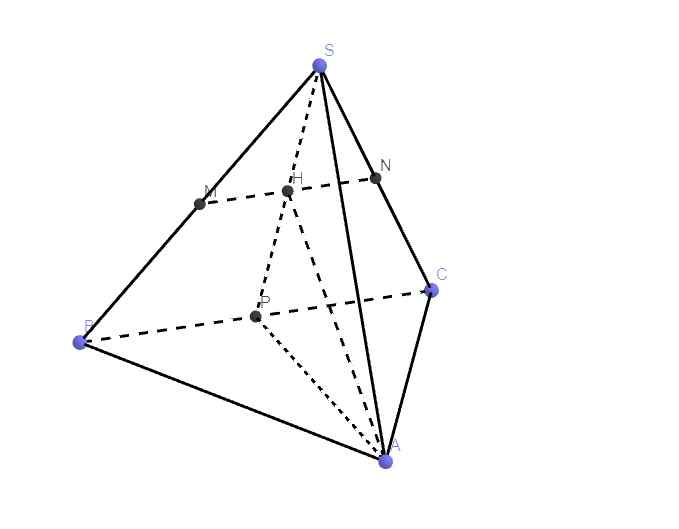
Gọi H là trung điểm MN \(\Rightarrow SH\perp MN\)
Do chóp SABC đều \(\Rightarrow\Delta AMN\) cân tại A \(\Rightarrow AH\perp MN\Rightarrow AH\perp\left(SBC\right)\)
\(\Rightarrow AH\perp SH\)
Nối SH kéo dài cắt BC tại P \(\Rightarrow\) P là trung điểm BC đồng thời H là trung điểm SP (Talet)
\(\Rightarrow\) AH là đường cao đồng thời là trung tuyến trong tam giác SAP
\(\Rightarrow\Delta SAP\) cân tại A
\(\Rightarrow SA=AP=\dfrac{a\sqrt{3}}{2}\)
\(SH=\dfrac{1}{2}\sqrt{SB^2-BP^2}=\dfrac{1}{2}\sqrt{SA^2-\left(\dfrac{a}{2}\right)^2}=\dfrac{a\sqrt{2}}{4}\)
\(MN=\dfrac{1}{2}BC=\dfrac{a}{2}\) ; \(HP=SH=\dfrac{a\sqrt{2}}{4}\)
\(AH=\sqrt{SA^2-SH^2}=\dfrac{a\sqrt{10}}{4}\)
\(V=\dfrac{1}{3}AH.\dfrac{1}{2}\left(MN+BC\right).HP=...\)