Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(U_{RC}=const=U\) khi \(Z_{L1}=2Z_C=R\)
Mặt khác L thay đổi để : \(U_{Lmax}:U_{Lmax}=\frac{U\sqrt{R^2+Z^2_C}}{R}=\frac{U\sqrt{2^2+1}}{2}=\frac{U\sqrt{5}}{2}\)
\(\Rightarrow chọn.D\)
+,có C=C1=>U_R=\frac{U.R}{\sqrt{R^2+(Zl-ZC1)^2}}
+,U R ko đổi =>Zl=ZC1
+,có c=C1/2=>ZC=2ZC1
=>U(AN)=U(RL)=\frac{U\sqrt{r^2+Z^2l}}{\sqrt{R^2+(Zl-2Z^2C1)}}=u=200V

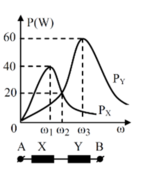
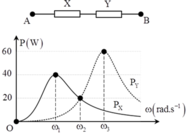
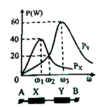
Từ đồ thị ta có: P Y max = 3 2 P X max ⇒ R X = 3 2 R Y
Mặc khác:
P X max = 2 P X ω 2 ⇔ U 2 R X = U 2 R X R X 2 + L 1 ω 2 − 1 C 1 ω 2 ⇒ L 1 ω 2 − 1 C 1 ω 2 = ± R 1
Ta chọn nghiệm L 1 ω 2 − 1 C 1 ω 2 = R X vì đồ thị P X tại giá trị ω 2 mạch đang có tính cảm kháng
Ta chọn nghiệm L 2 ω 2 − 1 C 2 ω 2 = − R Y vì đồ thị P Y tại giá trị ω 2 mạch đang có tính dung kháng
Công suất tiêu thụ của đoạn mạch AB tại ω 2 :
P = U 2 R 1 + R 2 R 1 + R 2 2 + L 1 + L 2 ω 2 − 1 C 1 + 1 C 2 1 ω 2 = U 2 R 2 1 + 3 2 1 + 3 2 2 + 3 2 − 2 2
Từ đó ta tính được P ω 2 = 23 , 97 W
Đáp án B

Ta có: \(U_L=U_C=\dfrac{U_R}{2}\)
\(\Rightarrow Z_L=Z_C=\dfrac{R}{2}=100\Omega\)
\(\Rightarrow R = 200\Omega\)
Tổng trở \(Z=R=200\Omega\) (do \(Z_L=Z_C\))
Cường độ dòng điện: \(I=\dfrac{U}{Z}=\dfrac{120}{200}=0,6A\)
Công suất: \(P=I^2.R=0,6^2.200=72W\)

Khi L1 và L2 mắc nối tiếp thì: U = U1 + U2 = - L1 didtdidt – L2 didtdidt
U = -(L1 + L2)didtdidt = −Ldidt−Ldidt với L = L1 + L2
Suy ra: ZL = Lω = L1ω + L2ω = ZL1ZL1 +

Lúc sau: \(P'=\frac{U^2.R^2}{R^2_2+Z^2_C}=\frac{U^2.R^2}{R^2_2+R_1R_2}=\frac{U^2}{R_1+R_2}=P=85W\)
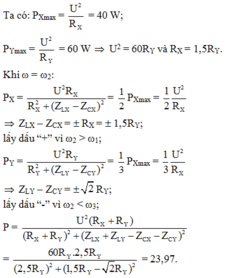
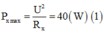
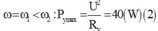
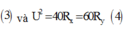

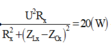
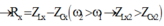
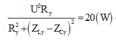
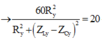
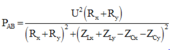
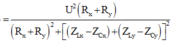

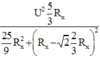
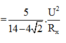
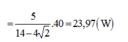
GIẢI THÍCH:
Chọn C.