Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

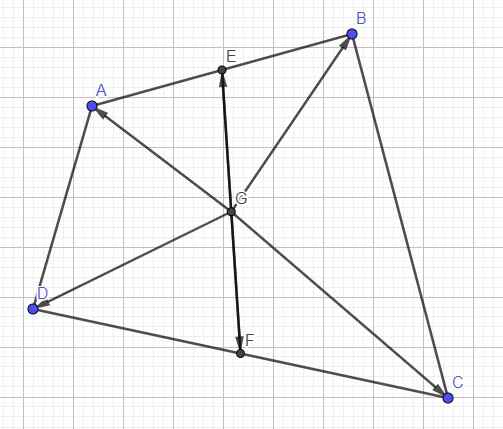
a.
E và F là trung điểm AB và CD nên: \(\overrightarrow{AB}=2\overrightarrow{AE}\) ; \(\overrightarrow{DC}=2\overrightarrow{DF}\)
G là trung điểm EF nên: \(\overrightarrow{AE}+\overrightarrow{AF}=2\overrightarrow{AG}\)
Do đó:
\(\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{AD}=2\overrightarrow{AE}+\overrightarrow{AD}+\overrightarrow{DC}+\overrightarrow{AD}=2\overrightarrow{AE}+2\overrightarrow{AD}+2\overrightarrow{DF}\)
\(=2\overrightarrow{AE}+2\left(\overrightarrow{AD}+\overrightarrow{DF}\right)=2\overrightarrow{AE}+2\overrightarrow{AF}=2\left(\overrightarrow{AE}+\overrightarrow{AF}\right)=4\overrightarrow{AG}\)
b.
\(\left(\overrightarrow{GA}+\overrightarrow{GB}\right)+\left(\overrightarrow{GC}+\overrightarrow{GD}\right)=2\overrightarrow{GE}+2\overrightarrow{GF}=2\left(\overrightarrow{GE}+\overrightarrow{GF}\right)=2.\overrightarrow{0}=\overrightarrow{0}\)
c.
Từ câu b ta có:
\(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}+\overrightarrow{GD}=\overrightarrow{0}\)
\(\Rightarrow\overrightarrow{GO}+\overrightarrow{OA}+\overrightarrow{OG}+\overrightarrow{OB}+\overrightarrow{GO}+\overrightarrow{OC}+\overrightarrow{GO}+\overrightarrow{OD}=\overrightarrow{0}\)
\(\Rightarrow4\overrightarrow{GO}+\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}=\overrightarrow{0}\)
\(\Rightarrow4\overrightarrow{OG}=\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}\)
\(\Rightarrow\overrightarrow{OG}=\dfrac{1}{4}\left(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}\right)\)

Lời giải:
Vì $M,N$ lần lượt là trung điểm của $AB,AC$ nên $MN$ là đường trung bình ứng với cạnh $BC$ của tam giác $ABC$
$\Rightarrow MN\parallel BC$ và $MN=\frac{1}{2}BC$
$\Rightarrow \overrightarrow{MN}=\frac{1}{2}\overrightarrow{BC}$
Mà:
$\overrightarrow{BP}=\frac{1}{2}\overrightarrow{BC}$ do $P$ là trung điểm $BC$
Do đó: $\overrightarrow{MN}=\overrightarrow{BP}$
---------------------------
Dễ chứng minh $NP$ là đường trung bình ứng với cạnh $AB$
$\Rightarrow \overrightarrow{PN}=\frac{1}{2}\overrightarrow{BA}$
Mà $M$ là trung điểm $AB$ nên $\overrightarrow{MA}=\frac{1}{2}\overrightarrow{BA}$
Vậy: $\overrightarrow{MA}=\overrightarrow{PN}$

a:Sửa đề: K nằm trên AC sao cho AK=1/3AC
\(\overrightarrow{BI}=\overrightarrow{BM}+\overrightarrow{MI}\)
\(=\dfrac{1}{2}\overrightarrow{BC}+\dfrac{1}{2}\overrightarrow{MA}\)
\(=\dfrac{1}{2}\overrightarrow{BC}-\dfrac{1}{2}\cdot\dfrac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{AC}\right)\)
\(=\dfrac{1}{2}\overrightarrow{BA}+\dfrac{1}{2}\overrightarrow{AC}-\dfrac{1}{4}\overrightarrow{AB}-\dfrac{1}{4}\overrightarrow{AC}\)
\(=-\dfrac{3}{4}\overrightarrow{AB}+\dfrac{1}{4}\overrightarrow{AC}\)
b: Gọi E là trung điểm của CK
=>AK=KE=CE
Xét ΔAME có AI/AM=AK/AE
nên IK//ME
Xét ΔBKC có CM/CB=CE/CK
nên ME//BK
IK//ME
ME//BK
Do đó: B,I,K thẳng hàng

a: vẽ vecto CN=vecto AB
(vecto AB;vecto CA)=(vecto CN;vecto CA)=góc ACN=120 độ
b: (vecto AB;vecto MC)
=(vecto CN;vecto CH)
=góc NCH
=120 độ

Câu 1: Chưa đủ dữ kiện để làm. Bạn xem lại đề.
Câu 2: Gọi tọa độ điểm H(a,b)
Ta có: \(\overrightarrow{AH}=(a-3; b-2); \overrightarrow{BC}=(1;8); \overrightarrow{BH}=(a-4; b+1); \overrightarrow{AC}=(2; 5)\)
Vì H là trực tâm tam giác ABC nên:
\(\left\{\begin{matrix} \overrightarrow{AH}.\overrightarrow{BC}=0\\ \overrightarrow{BH}.\overrightarrow{AC}=0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} a-3+8(b-2)=0\\ 2(a-4)+5(b+1)=0\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} a+8b=19\\ 2a+5b=3\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} a=\frac{-71}{11}\\ b=\frac{35}{11}\end{matrix}\right.\)

Bài 2:
a: Xét ΔOHA vuông tại A và ΔOHB vuông tại B có
OH chung
\(\widehat{AOH}=\widehat{BOH}\)
Do đó: ΔOHA=ΔOHB
Suy ra: HA=HB
hay ΔHAB cân tại H
b: Xét ΔOAB có
OH là đường cao
AD là đường cao
OH cắt AD tại C
Do đó: C là trực tâm của ΔOAB
Suy ra: BC\(\perp\)Ox
c: \(\widehat{HOA}=\dfrac{60^0}{2}=30^0\)
Xét ΔOHA vuông tại A có
\(\cos HOA=\dfrac{OA}{OH}\)
\(\Leftrightarrow OA=\dfrac{\sqrt{3}}{2}\cdot4=2\sqrt{3}\left(cm\right)\)
Câu 4:
Theo Cosy,ta được:
\(\left\{{}\begin{matrix}a+b>=2\sqrt{ab}\\ab+1>=2\sqrt{ab\cdot1}=2\sqrt{ab}\end{matrix}\right.\)
=>(a+b)(ab+1)>=4ab