
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Ptr hoành độ của `(P)` và `(d)` là:
`x^2=-5x-3m+1`
`<=>x^2+5x+3m-1=0` `(1)`
Để `(P)` cắt `(d)` tại `2` điểm phân biệt thì ptr `(1)` có `2` nghiệm phân biệt
`=>\Delta > 0`
`<=>5^2-4(3m-1) > 0`
`<=>25-12m+4 > 0`
`<=>m < 29/12`
`=>` Áp dụng Viét có: `{(x_1+x_2=-b/a=-5),(x_1.x_2=c/a=3m-1):}`
Ta có: `[x_1 ^2]/[x_2]-[x_2 ^2]/[x_1]+3=75/[x_1.x_2]`
`<=>[x_1 ^3-x_2 ^3]/[x_1.x_2]+[3x_1.x_2]/[x_1.x_2]=75/[x_1.x_2]`
`=>(x_1-x_2)(x_1 ^2+x_1.x_2+x_2 ^2)+3x_1.x_2=75`
`<=>(x_1-x_2)[(x_1+x_2)^2-x_1.x_2]+3x_1.x_2=75`
`<=>(x_1-x_2)[(-5)^2-3m+1]+3(3m-1)=75`
`<=>(x_1-x_2)(26-3m)=78-9m`
`<=>x_1-x_2=[3(26-3m)]/[26-3m]`
`<=>x_1-x_2=3`
Kết hợp với `x_1+x_2=-5`
Giải hệ `=>{(x_1=-1),(x_2=-4):}`
Thay vào `x_1.x_2=3m-1` có:
`-1.(-4)=3m-1`
`<=>m=5/3` (t/m)

Pt hoành độ giao điểm: \(x^2-mx-m-1=0\) (1)
(d) cắt (P) tại 2 điểm pb nằm về 2 phía trục tung khi (1) có 2 nghiệm pb trái dấu
\(\Leftrightarrow ac=-m-1< 0\Rightarrow m>-1\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=m\\x_1x_2=-m-1\end{matrix}\right.\)
\(y_1+y_2=50\)
\(\Leftrightarrow\left(mx_1+m+1\right)+\left(mx_2+m+1\right)=50\)
\(\Leftrightarrow m\left(x_1+x_2\right)+2m-48=0\)
\(\Leftrightarrow m^2+2m-48=0\Rightarrow\left[{}\begin{matrix}m=6\\m=-8\left(loại\right)\end{matrix}\right.\)

3b:
ĐKXĐ: \(x\in R\)
\(\sqrt{x^2+2x+4}+\left(x-1\right)\left(x+3\right)+1=0\)
=>\(\sqrt{x^2+2x+4}+x^2+2x-3+1=0\)
=>\(\sqrt{x^2+2x+4}+x^2+2x-2=0\)
=>\(x^2+2x+4+\sqrt{x^2+2x+4}-6=0\)
=>\(\left(\sqrt{x^2+2x+4}\right)^2+3\sqrt{x^2+2x+4}-2\sqrt{x^2+2x+4}-6=0\)
=>\(\left(\sqrt{x^2+2x+4}+3\right)\left(\sqrt{x^2+2x+4}-2\right)=0\)
=>\(\sqrt{x^2+2x+4}-2=0\)
=>\(\sqrt{x^2+2x+4}=2\)
=>\(x^2+2x+4=4\)
=>\(x^2+2x=0\)
=>x(x+2)=0
=>\(\left[{}\begin{matrix}x=0\\x+2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\left(nhận\right)\\x=-2\left(nhận\right)\end{matrix}\right.\)

Câu 1:
1) Ta có: \(2x^2+5x-3=0\)
\(\Leftrightarrow2x^2+6x-x-3=0\)
\(\Leftrightarrow\left(x+3\right)\left(2x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-3\\x=\dfrac{1}{2}\end{matrix}\right.\)
2) Để hàm số đồng biến trên R thì m-1>0
hay m>1
Câu 1:
3) Ta có: P=a+b-2ab
\(=1+\sqrt{2}+1-\sqrt{2}-2\left(1+\sqrt{2}\right)\left(1-\sqrt{2}\right)\)
\(=2-2\cdot\left(-1\right)=4\)

Bài 3:
b: Ta có: \(\sqrt{x^2-2x+1}=\left|x-2\right|\)
\(\Leftrightarrow\left|x-1\right|=\left|x-2\right|\)
\(\Leftrightarrow x-1=2-x\)
\(\Leftrightarrow2x=3\)
hay \(x=\dfrac{3}{2}\)
Bài 4: ĐK: x>0
a) \(B=\dfrac{x^2+\sqrt{x}}{x-\sqrt{x}+1}+1-\dfrac{2x+\sqrt{x}}{\sqrt{x}}\)
\(\Leftrightarrow B=\dfrac{\sqrt{x}\left[\left(\sqrt{x}\right)^3+1\right]}{x-\sqrt{x}+1}+1-\dfrac{\sqrt{x}\left(2\sqrt{x}+1\right)}{\sqrt{x}}\)
\(\Leftrightarrow B=\dfrac{\sqrt{x}.\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)}{x-\sqrt{x}+1}+1-2\sqrt{x}-1\)
\(\Leftrightarrow B=\sqrt{x}.\left(\sqrt{x}+1\right)-2\sqrt{x}=x+\sqrt{x}-2\sqrt{x}\)
\(\Leftrightarrow B=x-\sqrt{x}\)
Vậy với x>0 thì \(B=x-\sqrt{x}\)
b) Ta có: \(B=2\)
\(\Leftrightarrow x-\sqrt{x}=2\)
\(\Leftrightarrow x-\sqrt{x}-2=0\)
\(\Leftrightarrow x-2\sqrt{x}+\sqrt{x}-2=0\)
\(\Leftrightarrow\sqrt{x}.\left(\sqrt{x}-2\right)+\left(\sqrt{x}-2\right)=0\)
\(\Leftrightarrow\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)=0\)
Do \(\sqrt{x}+1>0\) nên, ta suy ra:
\(\sqrt{x}-2=0\Leftrightarrow\sqrt{x}=2\Leftrightarrow x=4\) \(\left(TMĐK\right)\)
Vậy \(x=4\) thì \(B=2\)

b: x1^2+m(x2)=13
=>x1^2+x2(x1+x2)=13
=>(x1+x2)^2-x1x2=13
=>m^2-m+1-13=0
=>m^2-m-12=0
=>m=4; m=-3

a) \(=\left|\sqrt{3}-3\right|+\sqrt{\left(\sqrt{3}-1\right)^2}=3-\sqrt{3}+\sqrt{3}-1=2\)
b) \(=\dfrac{\sqrt{5}+2}{5-4}-\dfrac{\sqrt{5}\left(\sqrt{2}-1\right)}{\sqrt{2}-1}=\sqrt{5}+2-\sqrt{5}=2\)

b) Gọi giao điểm của (d) với Ox là điểm A. \(\Rightarrow y=0.\)
\(\Rightarrow\) \(OA=\left|\dfrac{-4}{m}\right|=\dfrac{4}{\left|m\right|}.\) (đvđd).
Gọi giao điểm của (d) với Oy là điểm B. \(\Rightarrow x=0.\)
\(\Rightarrow OB=4\) (đvđd).
Ta có: \(S_{\Delta ABC}=\dfrac{1}{2}OA.OB=\dfrac{1}{2}.\dfrac{4}{\left|m\right|}.4=8\) (đvdt).
\(\Rightarrow\dfrac{4}{\left|m\right|}=4.\Leftrightarrow\left|m\right|=1.\Leftrightarrow\left[{}\begin{matrix}m=1.\\m=-1.\end{matrix}\right.\)






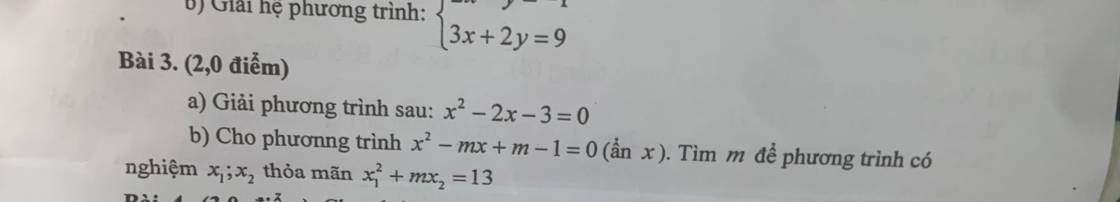
Bài 3:
\(b,\text{PT hoành độ giao điểm }\left(d_1\right);\left(d_2\right):\\ \dfrac{1}{4}x-6=5+3x\Leftrightarrow\dfrac{11}{4}x=-11\Leftrightarrow x=-4\Leftrightarrow y=-7\Leftrightarrow A\left(-4;-7\right)\\ \Leftrightarrow A\left(-4;-7\right)\in\left(d_3\right)\Leftrightarrow\left\{{}\begin{matrix}a=2\\-4a+b=-7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=2\\b=1\end{matrix}\right.\)