Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(U_{RC}=const=U\) khi \(Z_{L1}=2Z_C=R\)
Mặt khác L thay đổi để : \(U_{Lmax}:U_{Lmax}=\frac{U\sqrt{R^2+Z^2_C}}{R}=\frac{U\sqrt{2^2+1}}{2}=\frac{U\sqrt{5}}{2}\)
\(\Rightarrow chọn.D\)
+,có C=C1=>U_R=\frac{U.R}{\sqrt{R^2+(Zl-ZC1)^2}}
+,U R ko đổi =>Zl=ZC1
+,có c=C1/2=>ZC=2ZC1
=>U(AN)=U(RL)=\frac{U\sqrt{r^2+Z^2l}}{\sqrt{R^2+(Zl-2Z^2C1)}}=u=200V

Chọn đáp án A
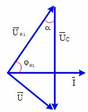
+ Khi 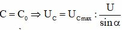
![]()
do Z L và R không đổi nên α và φ R L không đổi
+ Khi 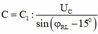
![]()
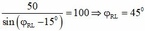
![]()
+ Khi 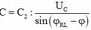
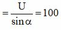
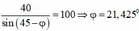
![]()

Khi Uc1=40V thì có Um= \(\sqrt{60^2+\left(120-40\right)^2}\)=100 V và UL=2Ur là không đổi
Khi U2=80V Thì Um=1002= Ur2 +(2Ur-80)2 Giải ra đk Ur= 73,76V

Bạn nên gửi mỗi câu hỏi một bài thôi để mọi người tiện trao đổi.
1. \(Z_L=200\sqrt{3}\Omega\), \(Z_C=100\sqrt{3}\Omega\)
Suy ra biểu thức của i: \(i=1,1\sqrt{2}\cos\left(100\pi t-\frac{\pi}{3}\right)A\)
Công suất tức thời: p = u.i
Để điện áp sinh công dương thì p > 0, suy ra u và i cùng dấu.
Biểu diễn vị trí tương đối của u và i bằng véc tơ quay ta có:
u u i i 120° 120°
Như vậy, trong 1 chu kì, để u, i cùng dấu thì véc tơ u phải quét 2 góc như hình vẽ.
Tổng góc quét: 2.120 = 2400
Thời gian: \(t=\frac{240}{360}.T=\frac{2}{3}.\frac{2\pi}{100\pi}=\frac{1}{75}s\)
2. Khi nối tắt 2 đầu tụ điện thì cường độ dòng điện hiệu dụng không đổi \(\Rightarrow Z_1=Z_2\Leftrightarrow Z_C-Z_L=Z_L\Leftrightarrow Z_C=2Z_L\)
\(U_C=1,2U_d\Leftrightarrow Z_C=2Z_d\Leftrightarrow Z_C=2\sqrt{R^2+Z_L^2}\)
\(\Leftrightarrow2Z_L=\sqrt{R^2+Z_L^2}\Leftrightarrow R=\sqrt{3}Z_L\)
Khi bỏ tụ C thì cường độ dòng điện của mạch là: \(I=\frac{U}{Z_d}=\frac{U}{\sqrt{R^2+Z_L^2}}=\frac{220}{\sqrt{3.Z_L^2+Z_L^2}}=0,5\)
\(\Rightarrow Z_L=220\Omega\)

\(U_c=IZ_c=\frac{U}{Z}.Z_c=\frac{U}{\sqrt{R^2+\left(Z_L-Z_C\right)^2}}.Z_c\)
\(=\frac{U}{\sqrt{R^2+Z_L^2}-2Z_LZ_C+Z_C^2}.Z_C=\frac{U}{\sqrt{1-\frac{2Z_L}{Z_C}+\frac{R^2+Z_L^2}{Z_C^2}}}\)
Đặt \(x=\frac{1}{Z_C}\) thì ta thu được hàm của Uc(x)
\(U_c=\frac{U}{\sqrt{\left(R^2+Z_L^2\right)x^2-2Z_Lx+1}}\)
Tìm x để Uc Max khi Mẫu min và khi \(x=-\frac{b}{2a}=\frac{2Z_L}{2.\left(R^2+Z_L^2\right)}=\frac{Z_L}{R^2+Z_{L^2}}\)
=> \(Z_C=\frac{R^2+Z_L^2}{Z_L}=\)
và Ucmax = \(U.\frac{\sqrt{R^2+Z_L^2}}{R}.\)
Bạn thay số và thu được kết quả

\(2LC\omega^2=1\rightarrow2Z_L=Z_C\rightarrow2u_L=-uc\)
\(u_m=u_R+u_L+u_c=40+\left(-30\right)+60=70V\)
Chọn B
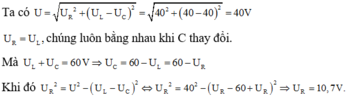
GIẢI THÍCH:
Chọn D.