
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a.
Trong tam giác A'BC ta có: I là trung điểm BA', M là trung điểm BC
\(\Rightarrow IM\) là đường trung bình tam giác A'BC
\(\Rightarrow IM||A'C\)
\(\Rightarrow IM||\left(ACC'A'\right)\)
Do \(A\in\left(AB'M\right)\cap\left(ACC'A'\right)\) và \(\left\{{}\begin{matrix}IM\in\left(AB'M\right)\\A'C\in\left(ACC'A'\right)\\IM||A'C\end{matrix}\right.\)
\(\Rightarrow\) Giao tuyến của (AB'M) và (ACC'A') là đường thẳng qua A và song song A'C
Qua A kẻ đường thẳng d song song A'C
\(\Rightarrow d=\left(AB'M\right)\cap\left(ACC'A'\right)\)
b.
I là trung điểm AB', E là trung điểm AM
\(\Rightarrow IE\) là đường trung bình tam giác AB'M \(\Rightarrow IE||B'M\) (1)
Tương tự ta có IN là đường trung bình tam giác AA'B' \(\Rightarrow IN||A'B'\) (2)
(1);(2) \(\Rightarrow\left(EIN\right)||\left(A'B'M\right)\)
c.
Trong mp (BCC'B'), qua K kẻ đường thẳng song song B'M lần lượt cắt BC và B'C' tại D và F
\(DF||B'M\Rightarrow DF||IE\Rightarrow DF\subset\left(EIK\right)\)
Trong mp (ABC), nối DE kéo dài cắt AB tại G
\(\Rightarrow G\in\left(EIK\right)\)
Trong mp (A'B'C'), qua F kẻ đường thẳng song song A'C' cắt A'B' tại H
Do IK là đường trung bình tam giác A'BC' \(\Rightarrow IK||A'B'\)
\(\Rightarrow FH||IK\Rightarrow H\in\left(EIK\right)\)
\(\Rightarrow\) Tứ giác DFHG là thiết diện (EIK) và lăng trụ
Gọi J là giao điểm BK và B'M \(\Rightarrow J\) là trọng tâm tam giác B'BC
\(\Rightarrow\dfrac{BJ}{BK}=\dfrac{2}{3}\)
Áp dụng talet: \(\dfrac{BM}{BD}=\dfrac{BJ}{BK}=\dfrac{2}{3}\Rightarrow BD=\dfrac{3}{2}BM=\dfrac{3}{2}.\dfrac{1}{2}BC=\dfrac{3}{4}BC\)
\(\Rightarrow MD=\dfrac{1}{4}BC=\dfrac{1}{2}CM\Rightarrow D\) là trung điểm CM
\(\Rightarrow DE\) là đường trung bình tam giác ACM
\(\Rightarrow DE||AC\Rightarrow DE||FH\)
\(\Rightarrow\) Thiết diện là hình thang

Do vai trò của 3 biến là như nhau, không mất tính tổng quát giả sử \(x>y>z\)
Ta có: \(x-z=\left(x-y\right)+\left(y-z\right)\)
Đặt \(\left\{{}\begin{matrix}x-y=a>0\\y-z=b>0\end{matrix}\right.\)
Do \(x;z\in\left[0;2\right]\Rightarrow x-z\le2\) hay \(a+b\le2\)
Ta có:
\(P=\dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{\left(a+b\right)^2}\ge\dfrac{1}{2}\left(\dfrac{1}{a}+\dfrac{1}{b}\right)^2+\dfrac{1}{\left(a+b\right)^2}\ge\dfrac{1}{2}\left(\dfrac{4}{a+b}\right)^2+\dfrac{1}{\left(a+b\right)^2}\)
\(P\ge\dfrac{9}{\left(a+b\right)^2}\ge\dfrac{9}{2^2}=\dfrac{9}{4}\)
Dấu "=" xảy ra khi \(\left\{{}\begin{matrix}a=b\\a+b=2\\\end{matrix}\right.\) \(\Rightarrow a=b=1\) hay \(\left(x;y;z\right)=\left(0;1;2\right)\) và các hoán vị

a.
\(90^0< a< 180^0\Rightarrow cosa< 0\)
\(\Rightarrow cosa=-\sqrt{1-sin^2a}=-\dfrac{2\sqrt{2}}{3}\)
\(tana=\dfrac{sina}{cosa}=-\dfrac{\sqrt{2}}{4}\)
b.
\(0< a< 90^0\Rightarrow cosa>0\)
\(\Rightarrow cosa=\sqrt{1-sin^2a}=\dfrac{4}{5}\)
\(tana=\dfrac{sina}{cosa}=\dfrac{3}{4}\)
\(cota=\dfrac{1}{tana}=\dfrac{4}{3}\)
c.
\(A=\dfrac{\dfrac{sina}{cosa}+\dfrac{3cosa}{sina}}{\dfrac{sina}{cosa}+\dfrac{cosa}{sina}}=\dfrac{sin^2a+3cos^2a}{sin^2a+cos^2a}=1+2cos^2a=\dfrac{17}{8}\)
d.
\(A=\dfrac{\dfrac{cosa}{sina}+\dfrac{3sina}{cosa}}{\dfrac{2cosa}{sina}+\dfrac{sina}{cosa}}=\dfrac{cos^2a+3sin^2a}{2cos^2a+sin^2a}=\dfrac{cos^2a+3\left(1-cos^2a\right)}{2cos^2a+\left(1-cos^2a\right)}\)
\(=\dfrac{3-2cos^2a}{1+cos^2a}=\dfrac{19}{13}\)

1: (SBD) và (SBC) cùng vuông góc (ABCD)
=>SB vuông góc BC và SB vuông góc AB
=>ΔSAB vuông tại B, ΔSBC vuông tại B
CD vuông góc SB
CD vuông góc BC
=>CD vuông góc (SBC)
=>CD vuông góc CS
=>ΔCSD vuông tại C
AD vuông góc BD
=>AD vuông góc SB
=>AD vuông góc (SBD)
=>AD vuông góc SD
=>ΔSDA vuông tại D
b: BCDE là hình vuông
=>CE vuông góc BD
mà CE vuông góc SB
nên CE vuông (SBD)
=>(SCE) vuông góc (SBD)
3: Kẻ BM//CE(M thuộc CD)
CE vuông góc SD
=>BM vuông góc SD
Kẻ MP vuông góc SD cắt SC tại N
=>BN vuông góc SD
Xét (SCE) kẻ NQ'//CE(Q' thuộc SE)
=>NQ' vuông góc SD
Kẻ BQ' cắt SA tại F
=>Thiết diện cần tìm là BNPF

Không gian mẫu: \(C_{100}^5\)
Trong 100 số từ 1 tới 100 có 50 số chẵn và 50 số lẻ
Để tổng 5 số là 1 số chẵn ta có các trường hợp: (5 số đều chẵn), (1 số chẵn 4 số lẻ), (3 số chẵn 2 số lẻ)
\(\Rightarrow C_{50}^5+C_{50}^1C_{50}^4+C_{50}^3C_{50}^2\) trường hợp thỏa mãn
Xác suất: \(P=\dfrac{C_{50}^5+C_{50}^1C_{50}^4+C_{50}^3C_{50}^2}{C_{100}^5}=...\)

Câu 7:
Xét hình bình hành ABCD, gọi O là giao của AC và BD
\(OB=OD=\dfrac{BD}{2}\Rightarrow BD=2OB\) (trong hbh 2 đường chéo cắt nhau tại trung điểm mỗi đường)
Ta có
\(BN=\dfrac{1}{3}BD\left(gt\right)\Rightarrow BN=\dfrac{1}{3}.2OB=\dfrac{2}{3}OB\)
Xét hbh ABEF, gọi I là giao của AE và BF ta có
\(IA=IE=\dfrac{AE}{2}\Rightarrow AE=2IA\) (trong hbh 2 đường chéo cắt nhau tại trung điểm mỗi đường)
Ta có
\(AM=\dfrac{1}{3}AE\left(gt\right)\Rightarrow AM=\dfrac{1}{3}.2IA=\dfrac{2}{3}IA\) (1)
Xét tg ABF có
\(IB=IF\) (trong hbh 2 đường chéo cắt nhau tại trung điểm mỗi đường) => IA là trung tuyến của tg ABF (2)
Từ (1) và (2) => M là trọng tâm của tg ABF
Gọi K là giao của BM với AF => BK là trung tuyến của tg ABF
\(\Rightarrow BM=\dfrac{2}{3}BK\)
Xét tg BOK có
\(BN=\dfrac{2}{3}OB\left(cmt\right)\Rightarrow\dfrac{BN}{OB}=\dfrac{2}{3}\)
\(BM=\dfrac{2}{3}BK\left(cmt\right)\Rightarrow\dfrac{BM}{BK}=\dfrac{2}{3}\)
\(\Rightarrow\dfrac{BN}{OB}=\dfrac{BM}{BK}=\dfrac{2}{3}\) => MN//OK (Talet đảo trong tam giác) (3)
Xét tg ACF có
BK là trung tuyến của tg ABF (cmt) => KA=KF
Ta có
OA=OC (trong hbh 2 đường chéo cắt nhau tại trung điểm mỗi đường)
=> OK là đường trung bình của tg ACF => OK//CF (4)
Từ (3) và (4) => MN//CF
mà \(CF\in\left(DCEF\right)\)
=> MN//(DCEF)

Trong mp (ABCD), nối AN kéo dài cắt BC kéo dài tại E
⇒E∈(SBC)⇒E∈(SBC)
Do AD song song BE, áp dụng Talet:
ANNE=NDNC=1⇒AN=NE⇒ANNE=NDNC=1⇒AN=NE⇒ N là trung điểm AE
⇒MN⇒MN là đường trung bình tam giác SAE
⇒MN//SE⇒MN//(SBC)
 câu 3 5c mn giúp em cần gấp lắm ạ
câu 3 5c mn giúp em cần gấp lắm ạ



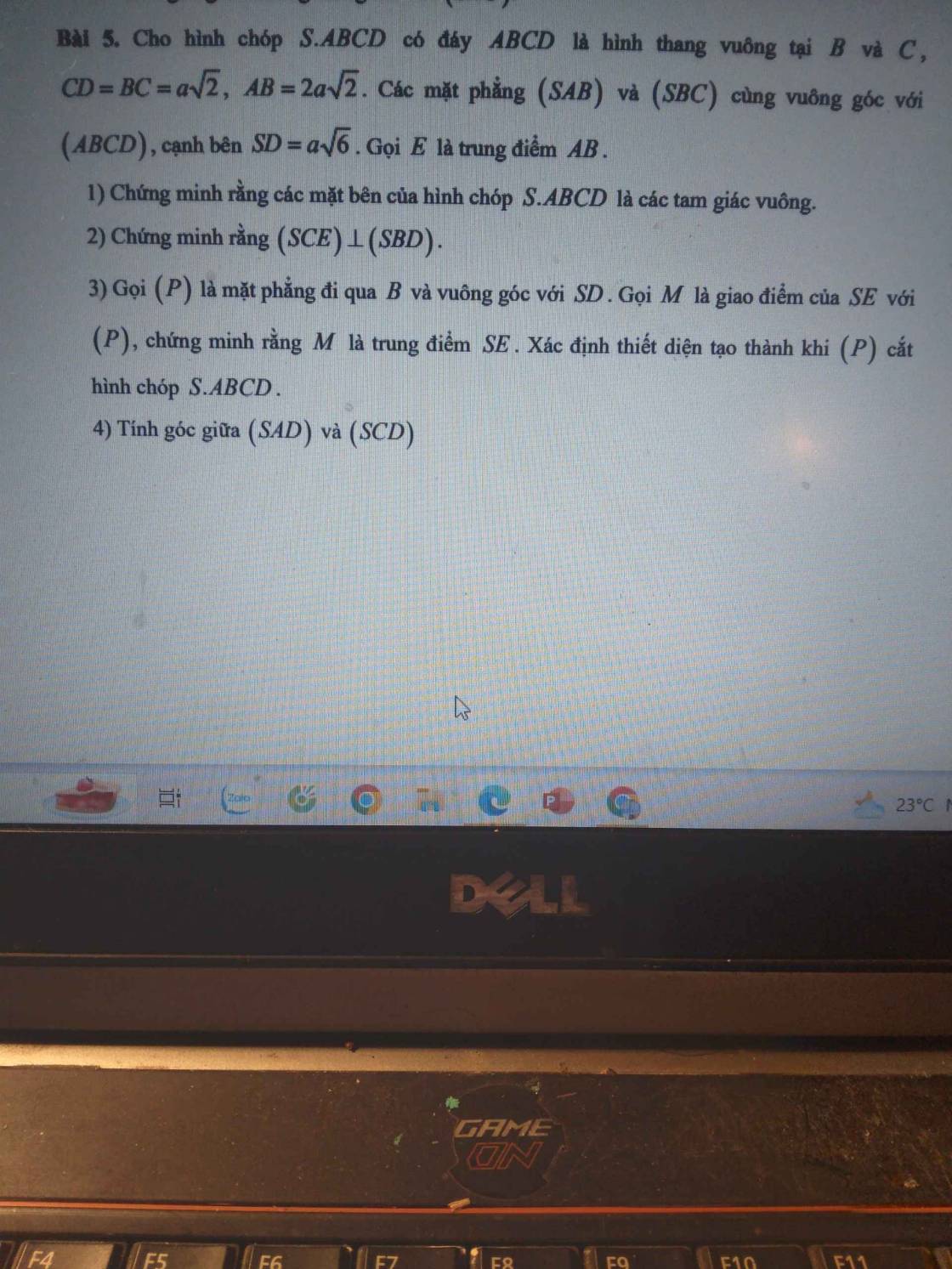 giúp em câu 3 4 với ạ. Cần gấp
giúp em câu 3 4 với ạ. Cần gấp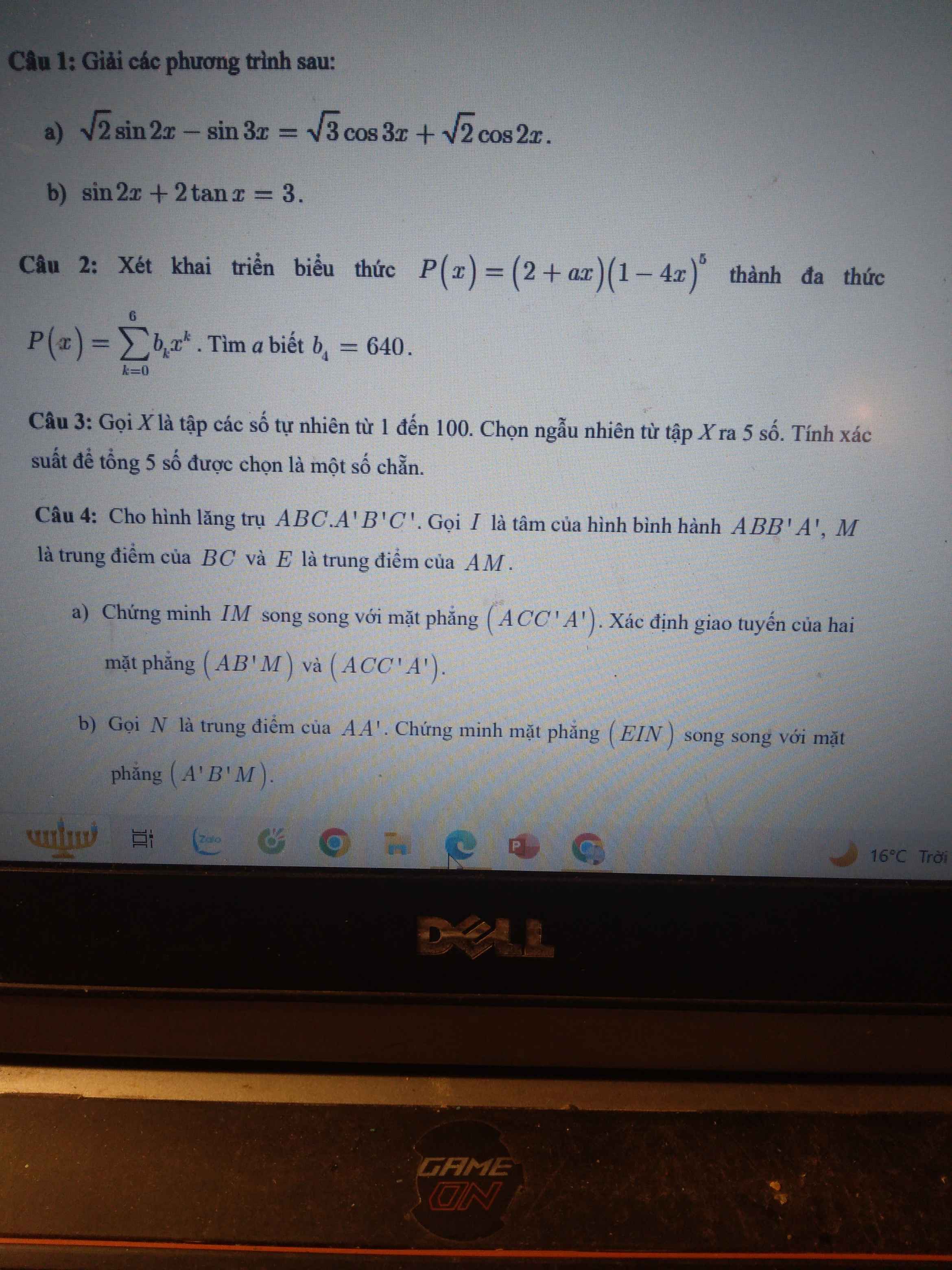

Qua D kẻ đường thẳng song song AC cắt BA kéo dài tại E
\(\Rightarrow BE=2BA=2a\)
\(AC||DE\Rightarrow AC||\left(SDE\right)\Rightarrow d\left(AC;SD\right)=d\left(AC;\left(SDE\right)\right)=d\left(A;\left(SDE\right)\right)\)
\(AE=AD=a\Rightarrow\Delta ADE\) vuông cân tại A
Gọi I là trung điểm DE \(\Rightarrow AI\perp DE\Rightarrow DE\perp\left(SAI\right)\)
Trong mp (SAI), kẻ \(AJ\perp SI\Rightarrow AJ\perp\left(SDE\right)\Rightarrow AJ=d\left(A;\left(SDE\right)\right)\)
\(AI=\dfrac{AD}{2}=\dfrac{\sqrt{AE^2+AD^2}}{2}=\dfrac{a\sqrt{2}}{2}\)
\(\dfrac{1}{AJ^2}=\dfrac{1}{AI^2}+\dfrac{1}{SA^2}\Rightarrow AJ=\dfrac{AI.SA}{\sqrt{AI^2+SA^2}}=\dfrac{a\sqrt{3}}{3}\)