Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(a,\\ \left(x+2\right)^2-x.\left(x-1\right)=10\\ \Leftrightarrow x^2+4x+4-x^2+x=10\\ \Leftrightarrow\left(x^2-x^2\right)+4x+x=10-4\\ \Leftrightarrow5x=6\\ \Leftrightarrow x=\dfrac{6}{5}\\ b,\\ x^3-6x^2+9x=0\\ \Leftrightarrow x.\left(x^2-6x+9\right)=0\\ \Leftrightarrow x.\left(x-3\right)^2=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x-3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=3\end{matrix}\right.\)

\(a,5x\left(x^2-9\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x^2=9\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=3\\x=-3\end{matrix}\right.\\ b,3\left(x+3\right)-x^2-3x=0\\ \Leftrightarrow3\left(x+3\right)-x\left(x+3\right)=0\\ \Leftrightarrow\left(x+3\right)\left(3-x\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=3\\x=-3\end{matrix}\right.\\ c,x^2-9x-10=0\\ \Leftrightarrow x^2+x-10x-10=0\\ \Leftrightarrow x\left(x+1\right)-10\left(x+1\right)=0\\ \Leftrightarrow\left(x-10\right)\left(x+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=-1\\x=10\end{matrix}\right.\)
a, 5\(x\)(\(x^2\) - 9) = 0
\(\left[{}\begin{matrix}x=0\\x^2-9=0\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=0\\x=3\\x=-3\end{matrix}\right.\)
Vậy \(x\) \(\in\) { -3; 0; 3}
b, 3.(\(x+3\)) - \(x^2\) - 3\(x\) = 0
3.(\(x+3\)) - \(x\).( \(x\) + 3) = 0
(\(x+3\))( 3 - \(x\)) = 0
\(\left[{}\begin{matrix}x=-3\\x=3\end{matrix}\right.\)
Vậy \(x\) \(\in\){ -3; 3}
c, \(x^2\) - 9\(x\) - 10 = 0
\(x^2\) + \(x\) - 10\(x\) - 10 = 0
\(x.\left(x+1\right)\) - 10.( \(x-1\)) = 0
(\(x+1\))(\(x-10\)) = 0
\(\left[{}\begin{matrix}x+1=0\\x-10=0\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=-1\\x=10\end{matrix}\right.\)
Vậy \(x\) \(\in\){ -1; 10}

a) ta có : \(\left(x-1\right)^3+3x\left(x-4\right)+1=0\)
\(\Leftrightarrow x^3-3x^2+3x-1+3x^2-12x+1=0\)
\(\Leftrightarrow x^3-9x=0\Leftrightarrow x\left(x-3\right)\left(x+3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x-3=0\\x+3=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=3\\x=-3\end{matrix}\right.\) vậy \(x=0;x=\pm3\)
b) \(x^2-25=6x-9\Leftrightarrow x^2-6x-16=0\)
\(\Leftrightarrow x^2+2x-8x-16=0\Leftrightarrow x\left(x+2\right)-8\left(x+2\right)=0\)
\(\Leftrightarrow\left(x-8\right)\left(x+2\right)=0\Leftrightarrow\left[{}\begin{matrix}x-8=0\\x+2=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=8\\x=-2\end{matrix}\right.\)
vậy \(x=8;x=-2\)
a )
\(\left(x-1\right)^3+3x\left(x-4\right)+1=0\)
\(\Leftrightarrow x^3-3x^2+3x-1+3x^2-12x+1=0\)
\(\Leftrightarrow x^3-9x=0\)
\(\Leftrightarrow x\left(x^2-9\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x^2-9=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x^2=9\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=\pm3\end{matrix}\right.\)
Vậy \(x\in\left\{0;\pm3\right\}\)
b )
\(x^2-25=6x-9\)
\(\Leftrightarrow x^2-6x=25-9\)
\(\Leftrightarrow x^2-6x=16\)
\(\Leftrightarrow x^2-6x-16=0\)
\(\Leftrightarrow x^2-2.x.3+9-25=0\)
\(\Leftrightarrow\left(x-3\right)^2=25\)
\(\Leftrightarrow\left[{}\begin{matrix}x-3=5\\x-3=-5\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=8\\x=-2\end{matrix}\right.\)
Vậy ...

a) 3x^3-12x=0
3x(x^2-4)=0
3x(x-2)(x+2)=0
suy ra 3x=0 suy ra x=0
x-2=0 x=2
x+2=0 x= -2
b) (x-3)^2-(x-3)(3-x)^2=0
(x-3)^2-(x-3)(x-3)^2=0
(x-3)^2(1-x+3)=0
(x-3)^2(4-x)=0
suy ra x-3=0 suy ra x=3
4-x=0 x=4
a) và b) đã nhé bạn

a)(x+2).(x+3)-(x-2).(x+5)=10
( x^2 +3x+2x+6)-(x^2 +5x-2x-10)=10
x^2 +3x+2x+6-x^2 -5x+2x+10-10=0
2x+6=0
2x=-6
x=-3

a) x² + 11x = 0
x(x + 11) = 0
x = 0 hoặc x + 11 = 0
*) x + 11 = 0
x = -11
Vậy x = -11; x = 0
b) (2x - 3)² - (x + 4)² = 0
(2x - 3 - x - 4)(2x - 3 + x + 4) = 0
(x - 7)(3x + 1) = 0
x - 7 = 0 hoặc 3x + 1 = 0
*) x - 7 = 0
x = 7
*) 3x + 1 = 0
3x = -1
x = -1/3
Vậy x = -1/3; x = 7
c) x² + 7x = 8
x² + 7x - 8 = 0
x² - x + 8x - 8 = 0
(x² - x) + (8x - 8) = 0
x(x - 1) + 8(x - 1) = 0
(x - 1)(x + 8) = 0
x - 1 = 0 hoặc x + 8 = 0
*) x - 1 = 0
x = 1
*) x + 8 = 0
x = -8
Vậy x = -8; x = 1

\(a)\)\(x^3-x^2-x+1=0\)
\(\Leftrightarrow\)\(x^2\left(x-1\right)-\left(x-1\right)=0\)
\(\Leftrightarrow\)\(\left(x-1\right)\left(x^2-1\right)=0\)
\(\Leftrightarrow\)\(\left(x-1\right)\left(x-1\right)\left(x+1\right)=0\)
\(\Leftrightarrow\)\(\left(x-1\right)^2\left(x+1\right)=0\)
\(\Leftrightarrow\)\(\orbr{\begin{cases}\left(x-1\right)^2=0\\x+1=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=1\\x=-1\end{cases}}}\)
Vậy \(x=1\) hoặc \(x=-1\)
Chúc bạn học tốt ~

\(x^2-3x+2.\left(x-3\right)=0\)
\(x.\left(x-3\right)+2.\left(x-3\right)=0\)
\(\left(x-3\right).\left(x+2\right)=0\)
\(\Rightarrow\orbr{\begin{cases}x=3\\x=-2\end{cases}}\)
\(x.\left(x-3\right)-3x+9=0\)
\(x.\left(x-3\right)-3.\left(x-3\right)=0\)
\(\left(x-3\right)^2=0=>x=3\)
a,\(x^2-3x+2\left(x-3\right)=0.\)
\(\Leftrightarrow x^2-3x+2x-6=0\)
\(\Leftrightarrow x^2+x-6=0\)
\(\Leftrightarrow\left(x^2-2x\right)+\left(3x-6\right)=0\)
\(\Leftrightarrow x\left(x-2\right)+3\left(x-2\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(x+3\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x-2=0\\x+3=0\end{cases}\Leftrightarrow}\orbr{\begin{cases}x=2\\x=-3\end{cases}}\)
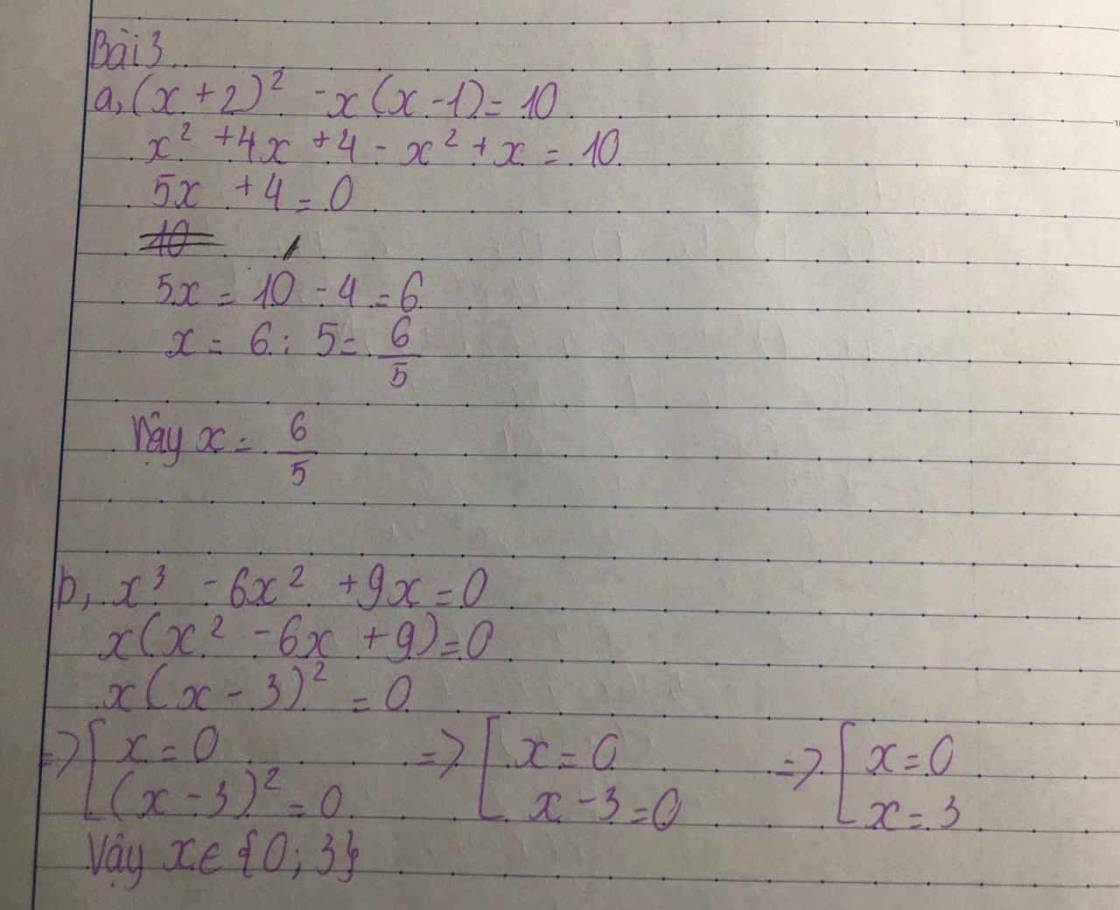
a.\(\left(x-1\right)^2+x\left(4-x\right)=11\)
\(\Leftrightarrow x^2-2x+1+4x-x^2=11\)
\(\Leftrightarrow2x=10\)
\(\Leftrightarrow x=5\)
b. \(x^2-9-2\left(x+3\right)=0\)
\(\Leftrightarrow x^2-9-2x-6=0\)
\(\Leftrightarrow x^2-2x-15=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=5\\x=-3\end{matrix}\right.\)
Em chú ý, dấu tương đương cuối cùng mình dùng ngoặc vuông (hoặc) chứ không dùng ngoặc nhọn (và) nhé.