
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu 22:
TXĐ: $(-\infty;0]\cup [2;+\infty)$
BPT \(\Leftrightarrow \left\{\begin{matrix} x\geq -1\\ x^2-2x\leq (x+1)^2\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\geq -1\\ x\geq \frac{-1}{4}\end{matrix}\right.\Leftrightarrow x\geq \frac{-1}{4}\)
Kết hợp ĐKXĐ suy ra BPT có nghiệm $[\frac{-1}{4};0]\cup [2;+\infty)$
Câu 23:
Theo công thức trung tuyến:
$CM^2=\frac{BC^2+AC^2}{2}-\frac{AB^2}{4}=\frac{23}{2}$
Áp dụng công thức Herong cho tam giác $ABC$:
$S_{ABC}=\sqrt{\frac{9}{2}(\frac{9}{2}-2)(\frac{9}{2}-3)(\frac{9}{2}-4)}=\frac{3\sqrt{15}}{4}$
$S_{BCM}=\frac{1}{2}S_{ABC}=\frac{3\sqrt{15}}{8}$
Áp dụng công thức: $S=\frac{abc}{4R}$ cho tam giác $BCM$ thì bán kính đường tròn ngoại tiếp tam giác là:
$R=\frac{BC.CM.BM}{4S_{BCM}}=\frac{4.\sqrt{\frac{23}{2}}.1}{\frac{3\sqrt{15}}{2}}=\frac{4\sqrt{690}}{45}$


Từ giả thiết suy ra:\(a^2=9\),\(c^2=1\) ,
-- > \(b^2=c^2-a^2=8\)
Vậy pt chính tắc của elip là : \(\dfrac{x^2}{9}+\dfrac{y^2}{8}=1\)
Ta chọn C


\(=\dfrac{-16}{5}\cdot\dfrac{-15}{64}+\left(\dfrac{4}{5}-2-\dfrac{4}{15}\right):\dfrac{47}{24}\)
\(=\dfrac{3}{4}-\dfrac{22}{15}\cdot\dfrac{24}{47}=\dfrac{1}{940}\)

Đặt x 2 = t ≥ 0 ta được t 2 + 1 − 3 t + 2 4 − 2 3 = 0
Ta có: Δ = 1 − 3 2 − 4.2 4 − 2 3
= 4 − 2 3 − 8 4 − 2 3 = − 7 4 − 2 3 < 0
Suy ra phương trình ẩn t vô nghiệm hay phương trình đã cho cũng vô nghiệm.
Đáp án cần chọn là: D




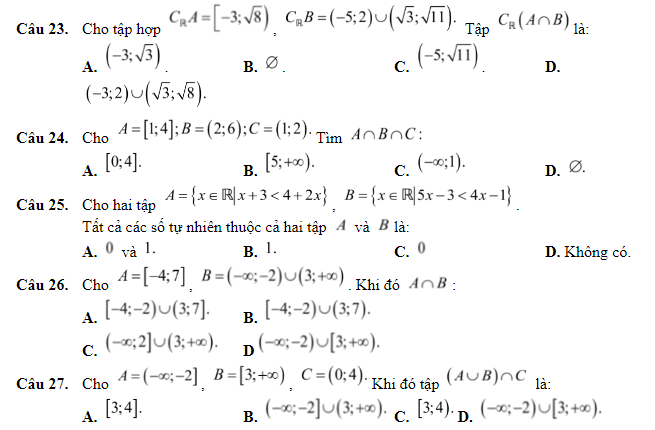




23.
\(\left|2x-1\right|>\left|x-2\right|\Leftrightarrow\left(2x-1\right)^2>\left(x-2\right)^2\)
\(\Leftrightarrow4x^2-4x+1>x^2-4x+4\)
\(\Leftrightarrow x^2>1\Rightarrow\left[{}\begin{matrix}x>1\\x< -1\end{matrix}\right.\)
24.
Do \(x^2+2x+1>0;\forall x\ne-1\) nên với \(x\ne-1\) BPT trở thành:
\(x^2-4x+3\le0\Rightarrow1\le x\le3\)