Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: \(\Delta ABO\sim\Delta A'B'O\Rightarrow\dfrac{AB}{A'B'}=\dfrac{OA}{OA'}\left(1\right)\)
Và \(\Delta OIF\sim\Delta A'B'F\Rightarrow\dfrac{OF}{A'F}=\dfrac{OI}{A'B'}\left(2\right)\)
\(\Rightarrow\dfrac{OF}{OF-OA'}=\dfrac{OA}{OA'}\Rightarrow\dfrac{12}{12-OA'}=\dfrac{6}{OA'}\Rightarrow OA'=4\left(cm\right)\)
Ta có: \(\dfrac{AB}{A'B'}=\dfrac{OA}{OA'}\Rightarrow A'B'=\dfrac{AB.OA}{OA'}=\dfrac{36.6}{4}=54\left(cm\right)\)
Vật ảnh cao 4cm và cách thấu kính 54cm

Khoảng cách từ ảnh đến thấu kính là:
Áp dụng công thức tính thấu kính:
\(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\Rightarrow d'=\dfrac{d.f}{d-f}=\dfrac{8.4}{8-4}=8\left(cm\right)\)
Chiều cao của ảnh:
Ta có: \(\dfrac{d}{d'}=\dfrac{h}{h'}\Rightarrow h'=\dfrac{d'.h}{d}=\dfrac{8.2}{8}=2\left(cm\right)\)

Ảnh thật, ngược chiều và lớn hơn vật.
Khoảng cách từ ảnh đến thấu kính:
\(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\Rightarrow\dfrac{1}{24}=\dfrac{1}{36}+\dfrac{1}{d'}\)
\(\Rightarrow d'=72cm\)

a) Vẽ ảnh theo đúng tỷ lệ
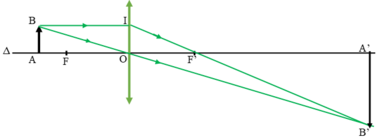
b) Trên hình vẽ, xét hai cặp tam giác đồng dạng:
ΔABO và ΔA’B’O; ΔA’B’F’ và ΔOIF’.
Từ hệ thức đồng dạng được:
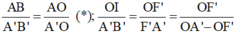
Vì AB = OI (tứ giác BIOA là hình chữ nhật)
![]()
↔ dd' – df = d'f (1)
Chia cả hai vế của (1) cho tích d.d’.f ta được:
![]()
(đây được gọi là công thức thấu kính cho trường hợp ảnh thật)
Thay d = 16cm, f = 12cm ta tính được: OA’ = d’ = 48cm
Thay vào (*) ta được:
![]()
Ảnh cao gấp 3 lần vật.
Để giải bài toán này, ta sẽ sử dụng công thức thấu kính hội tụ và các mối quan hệ giữa vật, ảnh, và thấu kính.
1. Dữ liệu bài toán:
2. Áp dụng công thức thấu kính hội tụ:
Công thức thấu kính hội tụ cho ta mối quan hệ giữa khoảng cách vật ��do, khoảng cách ảnh ��di, và tiêu cự �f như sau:
1�=1��+1��.f1=do1+di1.Thay các giá trị vào:
112=136+1��.121=361+di1.Giải phương trình để tìm ��di:
1��=112−136.di1=121−361.Tìm mẫu số chung là 36:
1��=336−136=236=118.di1=363−361=362=181.Vậy:
��=18 cm.di=18cm.3. Tính chiều cao ảnh:
Chiều cao ảnh được tính theo công thức tỷ lệ:
ℎ′ℎ=����.hh′=dodi.Thay giá trị vào:
ℎ′1=1836=12.1h′=3618=21.Vậy chiều cao ảnh là:
ℎ′=12 cm.h′=21cm.Kết quả:
\(tacó\Delta OAB\) ~\(\Delta OA^{\prime}B^{\prime}\left(g-g\right)\)
\(\frac{A^{\prime}B^{\prime}}{AB}=\frac{OA^{\prime}}{OA}\left(1\right)\)
\(\Delta FAB\) ~\(\Delta FOI\left(g-g\right)\)
\(\frac{A^{\prime}B^{\prime}}{AB}=\frac{OF}{OA-OF}\left(2\right)\)
Từ (1) và (2), ta có:
\(\frac{OA^{\prime}}{OA}=\frac{OF}{OA-OF}\)
\(\Rightarrow\frac{1}{OA}+\frac{1}{OA^{\prime}}=\frac{1}{OF}\)
\(\lrArr\frac{1}{36}+\frac{1}{OA^{\prime}}=\frac{1}{12}\)
\(\Rightarrow OA^{\prime}=18cm\)
Từ (1), ta có:
\(A^{\prime}B^{\prime}=\frac{OA^{\prime}}{OA}\cdot AB=\frac{18}{36}\cdot1=\frac12=0,5cm\)
Vậy khoảng cách từ ảnh đến thấu kính là 18 cm, chiều cao của ảnh là 0,5 cm