K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
KH
19 tháng 8 2021
Xin câu dễ :]] Hữu cơ hông chơi
Dùng phương pháp sunfat có thể điều chế được khí `HF,HCl` vì đây là 2 chất có tính oxi hoá và sẽ không tiếp tục tác dụng với \(H_2SO_{4\left(đ\right)}\) . Đối với 2 chất còn lại sẽ xảy ra phản ứng với \(H_2SO_{4\left(đ\right)}\)
\(NaF+H_2SO_{4\left(đ\right)}\underrightarrow{t^o}NaHSO_4+HF\)
\(NaCl+H_2SO_{4\left(đ\right)}\underrightarrow{t^o}NaHSO_4+HCl\)
\(2NaI+H_2SO_{4\left(đ\right)}\underrightarrow{t^o}Na_2SO_4+2HI\\ 8HI+H_2SO_{4\left(đ\right)}\underrightarrow{t^o}H_2S+4I_2+4H_2O\)
\(2NaBr+H_2SO_{4\left(đ\right)}\underrightarrow{t^o}Na_2SO_4+2HBr\\ 2HBr+H_2SO_{4\left(đ\right)}\underrightarrow{t^o}SO_2+Br_2+2H_2O\)
MH
10 tháng 1 2022
\(\sqrt{2+\sqrt{2}}.\sqrt{2-\sqrt{2}}\)
\(=\sqrt{\left(2+\sqrt{2}\right)\left(2-\sqrt{2}\right)}\)
\(=\sqrt{2^2-\left(\sqrt{2}\right)^2}=\sqrt{4-2}=\sqrt{2}\)
18 tháng 7 2015
2 công nhân làm cùng cv trong 4 ngày
\(\rightarrow\)1 ngày làm 1/4 công việc
người thứ 1 làm mất 6 ngày
\(\rightarrow\)1 ngày làm 1/6 công việc
gọi a là số công việc người 2 lm trong 1 ngày
ta có pt \(\frac{1}{4}=\frac{1}{6}+a\)---> \(a=\frac{1}{12}\)
----> người 2 lm hết cv trong 12 ngày
mình ko hiểu câu hỏi b cko lắm
NV
Nguyễn Việt Lâm
Giáo viên
6 tháng 3 2023
Ta có:
\(\dfrac{ab+bc+ca}{2\left(a^2+b^2+c^2\right)}+\dfrac{1}{6}\left(\dfrac{a^2+b^2+c^2}{abc}\right)\ge2\sqrt{\dfrac{1}{12}\left(\dfrac{ab+ca+ca}{abc}\right)}=\sqrt{3\left(\dfrac{ab+bc+ca}{abc}\right)}\)
Nên ta chỉ cần cm:
\(\sqrt{\dfrac{1}{3}\left(\dfrac{ab+bc+ca}{abc}\right)}\ge\dfrac{a+b+c}{3}\Leftrightarrow3\left(\dfrac{ab+bc+ca}{abc}\right)\ge\left(a+b+c\right)^2\)
Thật vậy, ta có:
\(\dfrac{3\left(ab+bc+ca\right)}{abc}=\dfrac{\left(a^2b+b^2c+c^2a\right)\left(ab+bc+ca\right)}{abc}\)
\(=\left(\dfrac{a}{c}+\dfrac{b}{a}+\dfrac{c}{b}\right)\left(ac+ab+bc\right)\ge\left(a+b+c\right)^2\) (Bunhiacopxki)
Dấu "=" xảy ra khi \(a=b=c=1\)
CT
0
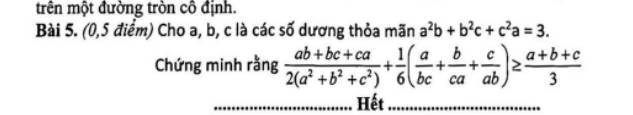
Bài nào?????????????????
full rồi
ae mình chiều nay sẽ lu hết chúng nó trên học thêm
Câu 20 cậu đưa VT về một bình phương cộng với cái chừa ra (hệ số nhân với y^2).
Thêm bớt cái mà đề bài yêu cầu CM sau đó dùng BUNHIACOPXKI.
(khó nói quá)