
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1: ĐKXĐ: 2-3x>=0
=>x<=2/3
2: ĐKXĐ: -3x^2>=0
=>x^2<=0
=>x=0
3: ĐKXĐ: -2023x^3>=0
=>x^3<=0
=>x<=0
4: ĐKXĐ: -2(x-5)>=0
=>x-5<=0
=>x<=5
5: ĐKXĐ: -5/2-2x>=0
=>2-2x<0
=>2x>2
=>x>1
6: ĐKXĐ: (x^2+1)(3-2x)>=0
=>3-2x>=0
=>-2x>=-3
=>x<=3/2
7: ĐKXĐ: (-x^2-1)(3-x)>=0
=>(x^2+1)(x-3)>=0
=>x-3>=0
=>x>=3

Câu 3 :
\(1,\left\{{}\begin{matrix}\dfrac{3}{\sqrt{y-2}}+x-2y=5\\\dfrac{1}{\sqrt{y-2}}-2x+4y=4\end{matrix}\right.\) \(\left(ĐK:y>2\right)\) \(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{3}{\sqrt{y-2}}+x-2y=5\\\dfrac{1}{\sqrt{y-2}}-2\left(x-2y\right)=4\end{matrix}\right.\) Đặt : \(\left\{{}\begin{matrix}a=\dfrac{1}{\sqrt{y-2}}\\b=x-2y\end{matrix}\right.\)
Ta có Hpt trở thành : \(\left\{{}\begin{matrix}3a+b=5\\a-2b=4\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}a=2\\b=-1\end{matrix}\right.\)\(\Rightarrow\left\{{}\begin{matrix}\dfrac{1}{\sqrt{y-2}}=2\\x-2y=-1\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}2\sqrt{y-2}=1\\x-2y=-1\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{5}{4}\\x-2.\dfrac{5}{4}=-1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{3}{2}\\y=\dfrac{5}{4}\end{matrix}\right.\)
Vậy ....
\(2,x^2-\left(2m+1\right)+m^2-m+1=0\left(1\right)\)
a, Thay m = 2 vào pt (1) có : \(x^2-5x+3=0\)
\(\Delta=5^2-4.3=13>0\Rightarrow\sqrt{\Delta}=\sqrt{13}\)
⇒ Phương trình có hai nghiệm phân biệt
\(x_1=\dfrac{5+\sqrt{13}}{2};x_2=\dfrac{5-\sqrt{13}}{2}\)
Vậy \(S=\left\{\dfrac{5\pm\sqrt{13}}{2}\right\}\) khi \(m=2\)
b, Để phương trình có hai nghiệm phân biệt thì \(\Delta>0\)
\(\Rightarrow\left(2m+1\right)^2-4m^2+4m-4>0\Leftrightarrow4m^2+4m+1-4m^2+4m-4>0\Leftrightarrow8m-3>0\Leftrightarrow m>\dfrac{3}{8}\)
Vậy...
2:
Gọi số cần tìm là \(\overline{ab}\)
Theo đề, ta có: a-b=3 và a^2+b^2=45
=>a=b+3 và (b+3)^2+b^2=45
=>b=3
=>a=6

câu 2 phần 2:
\(\left\{{}\begin{matrix}4x+3y=11\\4x-y=7\end{matrix}\right.\)\(< =>\left\{{}\begin{matrix}4y=4\\4x-y=7\end{matrix}\right.< =>\left\{{}\begin{matrix}y=1\\x=2\end{matrix}\right.\).Vậy hệ pt có nghiệm
(x,y)=(2;1)
caau3 phần 2:
\(x^2-2x+m-1=0\)(1)
\(\Delta'=\left(-1\right)^2-\left(m-1\right)=1-m+1=2-m\)
để pt (1) có 2 nghiệm x1,x2<=>\(\Delta'\ge0< =>2-m\ge0< =>m\le2\)
theo vi ét=>\(\left\{{}\begin{matrix}x1+x2=2\left(1\right)\\x1.x2=m-1\left(3\right)\end{matrix}\right.\)
có: \(x1^4\)\(-x1^3=x2^4-x2^3\)
\(< =>x1^4-x2^4-x1^3+x2^3=0\)
\(< =>\left(x1^2-x2^2\right)\left(x1^2+x2^2\right)-\left(x1^3-x2^3\right)\)\(=0\)
\(< =>\left(x1-x2\right)\left(x1+x2\right)\left[\left(x1+x2\right)^2-2x1x2\right]\)\(-\left(x1-x2\right)\left(x1^2+x1x2+x^2\right)=0\)
\(< =>\)\(\left(x1-x2\right)\left[2.2^2-2\left(m-1\right)-\left(x1^2+x1x2+x2^2\right)\right]=0\)
\(< =>.\left(x1-x2\right)\left[8-2m+2-\left(x1+x2\right)^2+x1x2\right]=0\)
<=>\(\left(x1-x2\right)\left[10-2m-4+m-1\right]=0\)
\(< =>\left(x1-x2\right)\left(5-m\right)=0\)
\(=>\left[{}\begin{matrix}x1-x2=0\\5-m=0\end{matrix}\right.< =>\left[{}\begin{matrix}x1=x2\left(2\right)\\m=5\left(loai\right)\end{matrix}\right.\)
thế(2) vào(1)=>\(x1=x2=1\left(4\right)\)
thế (4) vào (3)=>\(m-1=1=>m=2\left(TM\right)\)
vậy m=2 thì....

Câu 1:
\(a^2+2ab+b^2-ac-bc\)
\(=\left(a+b\right)^2-c\left(a+b\right)\)
\(=\left(a+b\right)\left(a+b-c\right)\)
Câu 2:
\(5x^2-5y^2-10x+10y\)
\(=5\left(x-y\right)\left(x+y\right)-10\left(x-y\right)\)
\(=\left(x-y\right)\left(5x+5y-10\right)\)
\(=5\left(x-y\right)\left(x+y-2\right)\)
Câu 3:
\(3x^2-6xy+3y^2-12z^2\)
\(=3\left[\left(x-y\right)^2-4z^2\right]\)
\(=3\left(x-y-2z\right)\left(x-y+2z\right)\)
Câu 4:
\(x^4+x^3+x^2-1\)
\(=x^3\left(x+1\right)+\left(x-1\right)\left(x+1\right)\)
\(=\left(x+1\right)\left(x^3+x-1\right)\)
Câu 5:
\(x^3-3x^2+3x-1-y^3\)
\(=\left(x-1\right)^3-y^3\)
\(=\left(x-1-y\right)\left[\left(x-1\right)^2+\left(x-1\right)y+y^2\right]\)
\(=\left(x-y-1\right)\left(x^2-2x+1+xy-y+y^2\right)\)
Câu 6:
\(x^4-x^2+2x-1\)
\(=x^4-\left(x-1\right)^2\)
\(=\left(x^2-x+1\right)\left(x^2+x-1\right)\)
Câu 7:
\(\left(x+y\right)^3-x^3-y^3\)
\(=\left(x+y\right)^3-\left[\left(x+y\right)^3-3xy\left(x+y\right)\right]\)
\(=3xy\left(x+y\right)\)

2:
a: Khi m=0 thì (1) sẽ là \(x^2-4=0\)
=>x=2 hoặc x=-2
b: x1^2+x2^2=20
=>(x1+x2)^2-2x1x2=20
=>(2m)^2-2(-m^2-4)=20
=>4m^2+2m^2+8=20
=>6m^2=12
=>m^2=2
=>\(m=\pm\sqrt{2}\)


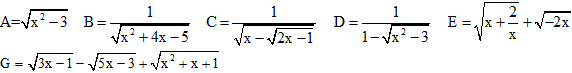 Mn giúp em với ;-;
Mn giúp em với ;-; giúp mình câu 4 với câu 2 phần 2 với
giúp mình câu 4 với câu 2 phần 2 với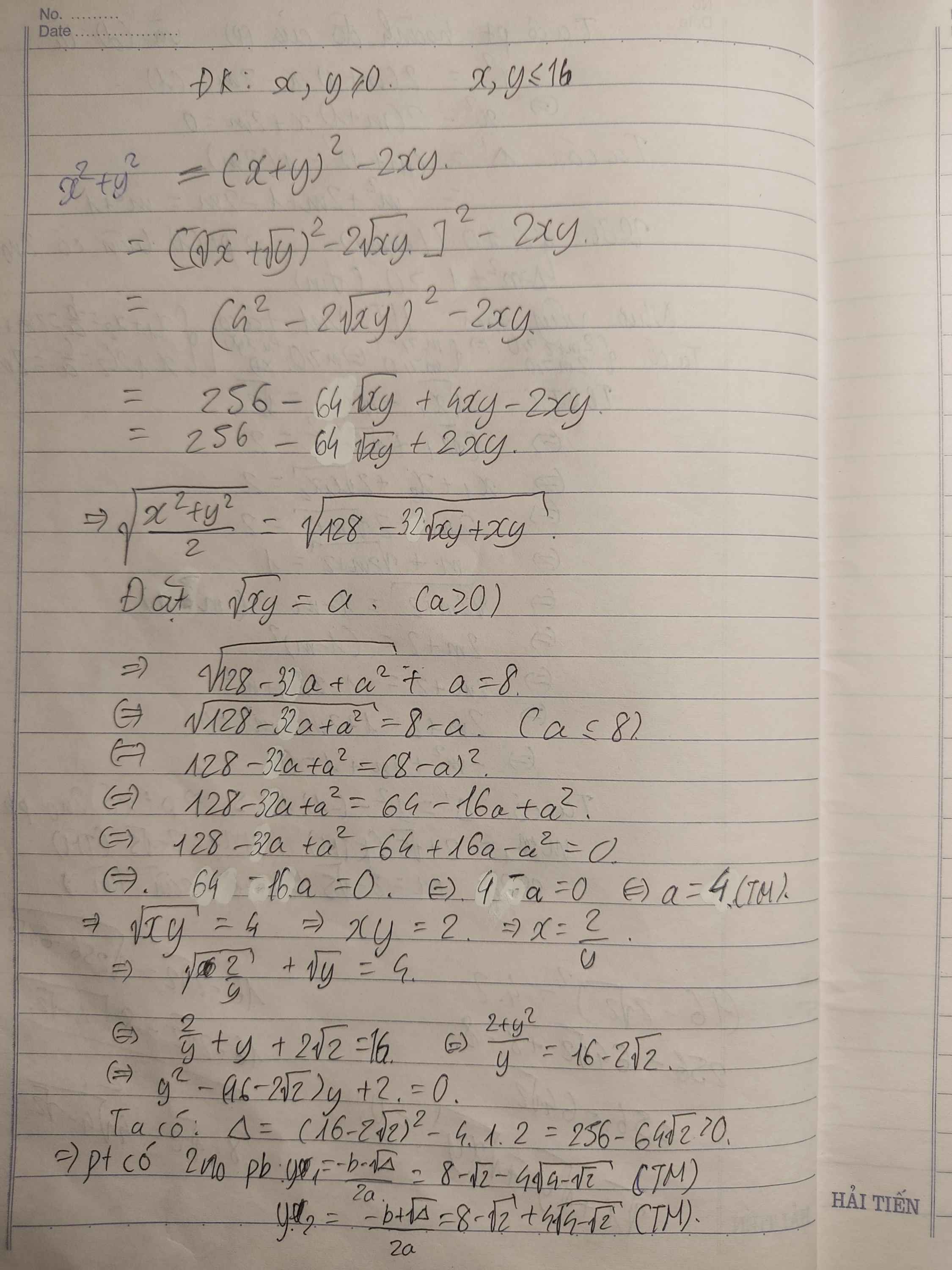
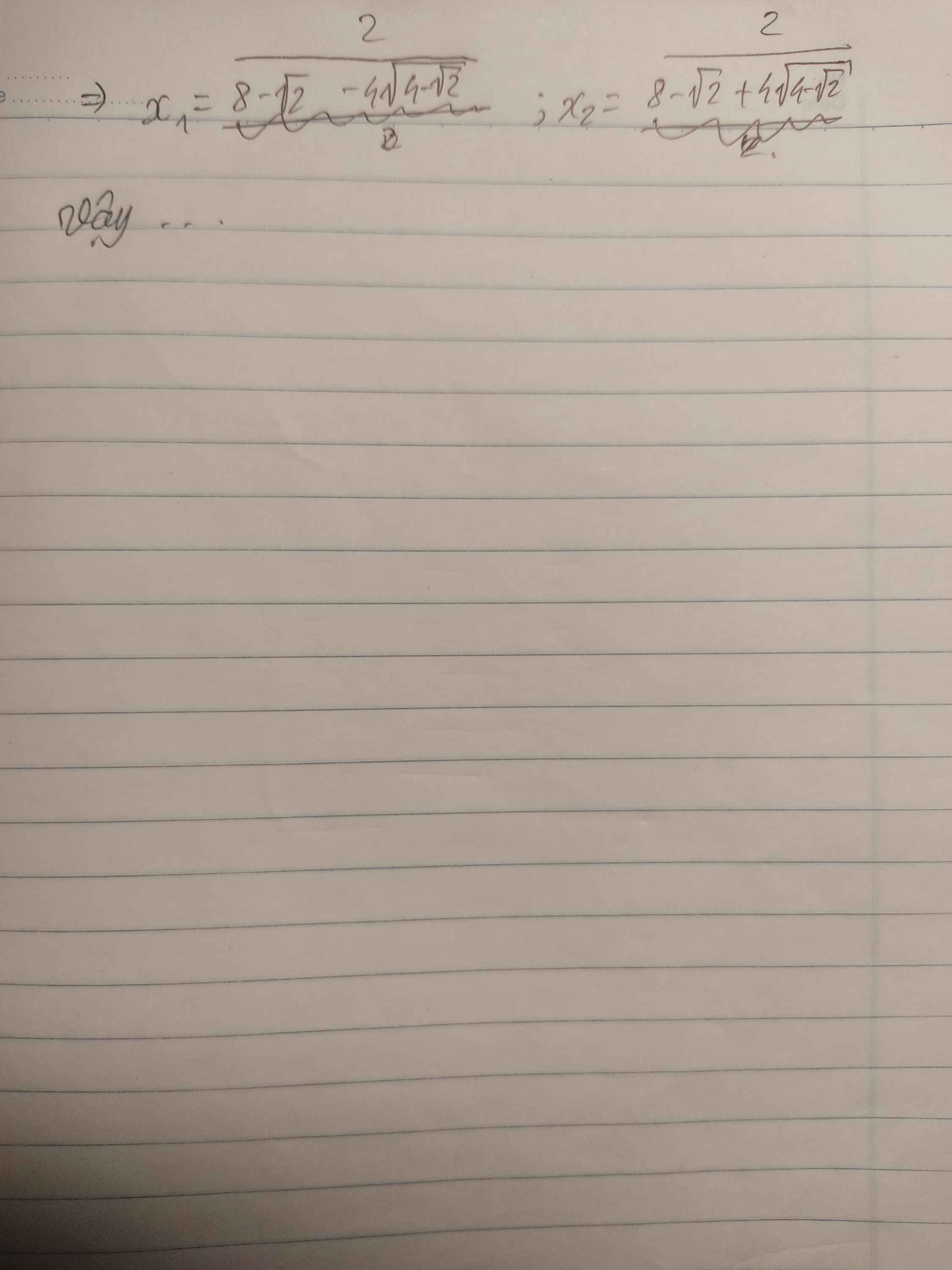

bài đâu bạn??
cô biết