K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

CM
11 tháng 1 2017
Chọn A.

Xác định được
![]()
Vì M là trung điểm SA nên
![]()
Kẻ AK ⊥ DM và chứng minh được AK ⊥ (CDM) nên
![]()
Trong tam giác vuông MAD tính được
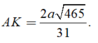

CM
9 tháng 1 2019
Đáp án C
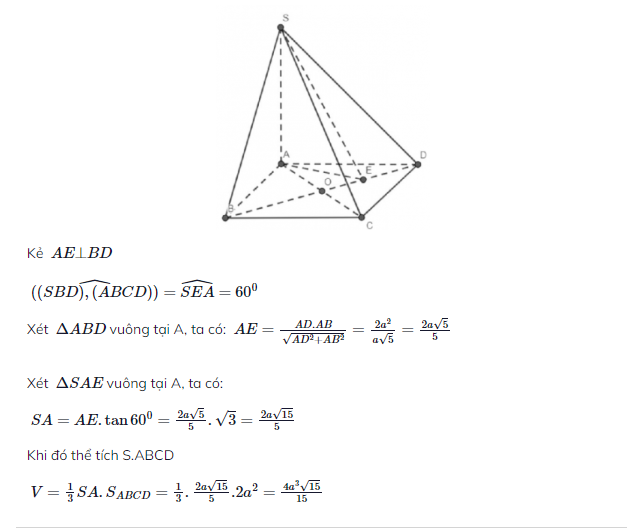
Kẻ AH ⊥BD
Khi đó ![]()
![]()
Mà ![]() nên góc giữa (SBD) và (ABCD) là SHA=α.
nên góc giữa (SBD) và (ABCD) là SHA=α.
Suy ra 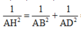
![]()
![]()
Do đó ![]()

NV
Nguyễn Việt Lâm
Giáo viên
8 tháng 3 2022
Đề bài thiếu độ dài SD hoặc dữ kiện để tính độ dài SD nên ko thể tính được góc giữa SA và (ABCD)
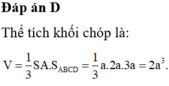
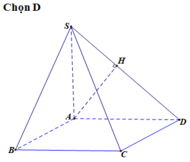


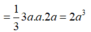



Mặt phẳng (BCM) // AD nên nó cắt mặt phẳng (SAD) theo giao tuyến MN//AD
Ta có: BC ⊥ AB và BC ⊥ SA => BC ⊥ BM
Tứ giác BCNM là hình thang vuông BM là đường cao.
có : BC \(\perp\) AB và BC \(\perp\) SA \(\Rightarrow\) BC \(\perp\) BM
Tứ giác BCNM là hình thang vuông BM là đường cao
ta có : SA = AB . tan 60 = \(a\sqrt{3}\)
\(\dfrac{MN}{AD}=\dfrac{SM}{SA}\)
\(\dfrac{MN}{2a}=\dfrac{a\sqrt{3}-\dfrac{a\sqrt{3}}{3}}{a\sqrt{3}}=\dfrac{2}{3}\)
\(\Rightarrow MN=\dfrac{4a}{3}\)
\(BM=\sqrt{a^2+\dfrac{a^2}{3}}\) \(=\dfrac{2a}{\sqrt{3}}\)
diện tích hình thang BCNM là : \(S=\dfrac{2a+\dfrac{4a}{3}}{2}.\dfrac{2a}{\sqrt{3}}=\dfrac{10a^2}{3\sqrt{3}}\)
\(V_{SBCNM}=\dfrac{1}{3}.SH.S_{BCNM}\)
Hạ SH ⊥ BM
ta có : SH \(\perp\) BM
và BC \(\perp\) (SAB) \(\equiv\) (SBM) \(\Rightarrow\) BC \(\perp\) SH . vậy SH \(\perp\) (BMNC)
\(\Rightarrow\) SH là đường cao của khối chóp S.BCNM
trong \(\Delta SBA\) có \(SB=\dfrac{AB}{cos60}=2a\)
\(\Rightarrow\) \(\dfrac{AB}{SB}=\dfrac{AM}{MS}=\dfrac{1}{2}\)
BM là phân giác của góc : \(\left\{{}\begin{matrix}SBH=gt\\SBH=30^o=gt\\SH=SB.sin30^o=2a.\dfrac{1}{2}=a\end{matrix}\right.\)
\(\Leftrightarrow\) thể tích khói chóp S.BCNM là :
\(V=\dfrac{1}{3}.a.\dfrac{10a^2}{3\sqrt{3}}=\dfrac{10\sqrt{3a^2}}{27}\)