Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Ket qua to1 lam duoc trong thang dau la420 sp
To2 lam duoc300sp
Gọi số thợ cần thiết là x (người),x ∈ N* , thời gian cần thiết là y (ngày), y > 0.
Coi toàn bộ công việc như một đơn vị công việc, thì một người thợ trong 1 ngày làm được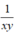 
( công việc).
Nếu giảm đi 3 người thì thời gian kéo dài 6 ngày. Như vậy, x – 3 người làm trong y + 6 ngày thì xong công việc. Do đó, ta có phương trình:
Nếu tăng thêm 2 người thì xong sớm 2 ngày. Như vậy, x + 2 người làm trong y – 2 ngày thì xong công việc. Do đó, ta có phương trình:
Từ (1) và (2) ta có hệ phương trình:
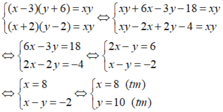
Vậy cần 8 người làm trong 10 ngày thì xong công việc.
Gọi số thợ và số ngày lần lượt là a,b
Theo đề, ta có hệ:
(a-3)(b+6)=ab và (a+2)(b-2)=ab
=>ab+6a-3b-18=ab và ab-2a+2b-4=ab
=>6a-3b=18 và -2a+2b=4
=>a=8 và b=10
- Gọi số người thợ ban đầu và số ngày cần làm theo quy định lần lượt là x (người) và y (ngày), (điều kiện cậu tự viết nhé)
- Từ đó ta có số công việc cân làm là : xy (công việc)
- Khi giảm 3 người thợ thì ta còn lại : x -3 (người)
- Khi thời gian phải kéo dài thêm 6 ngày thì tổng số ngày làm để xong việc là : y + 6 (ngày)
- Khi giảm 3 người thợ thì kéo dài thêm 6 ngày, mà số lượng công việc khong đổi nên ta có phương trình :
(x - 3).(y + 6) = xy <=> 6x - 3y = 18 (1)
/tăng thêm 2 người, xong sớm 2 ngày cũng làm tượng tự như vậy nha/ Từ đó ta có phương trình:
(x +2).(y - 2) = xy <=> -2x + 2y = 4 (2)
/từ chỗ này thì cậu tự giải hệ phương trình nha/
a/ Đặt \(x^2+65=k^2\) (\(k\in N\))
\(\Rightarrow k^2-x^2=65\)
\(\Rightarrow\left(k-x\right)\left(k+x\right)=65\)
\(\Rightarrow\left\{{}\begin{matrix}k-x=5\\k+x=13\end{matrix}\right.\) \(\Rightarrow2x=8\Rightarrow x=4\)
b/ Ta có \(8\equiv1\left(mod7\right)\Rightarrow8^n\equiv1\left(mod7\right)\)
\(\Rightarrow8^n+6\equiv7\left(mod7\right)\Rightarrow\left(8^n+6\right)⋮7\)
c/ Gọi số thợ và số ngày quy định là \(x;y\)
Theo bài ra ta có hệ:
\(\left\{{}\begin{matrix}\left(x-3\right)\left(y+6\right)=xy\\\left(x+2\right)\left(y-2\right)=xy\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}6x-3y=18\\-2x+2y=4\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=8\\y=10\end{matrix}\right.\)