Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Áp dụng định lý Pitago:
\(AB=\sqrt{BC^2+AC^2}=15\left(cm\right)\)
\(sinA=\dfrac{BC}{AB}=\dfrac{12}{15}=\dfrac{4}{5}\)
\(cosB=\dfrac{BC}{AB}=\dfrac{4}{5}\)
\(tanA=\dfrac{BC}{AC}=\dfrac{12}{9}=\dfrac{4}{3}\)
\(cotB=\dfrac{BC}{AC}=\dfrac{4}{3}\)
Áp dụng định lí Pytago vào ΔABC vuông tại C, ta được:
\(AB^2=CA^2+CB^2\)
\(\Leftrightarrow AB^2=9^2+12^2=225\)
hay AB=15(cm)
Xét ΔABC vuông tại C có
\(\sin\widehat{A}=\dfrac{CB}{AB}=\dfrac{12}{15}=\dfrac{4}{5}\)
\(\cos\widehat{B}=\dfrac{CB}{AB}=\dfrac{12}{15}=\dfrac{4}{5}\)
\(\tan\widehat{A}=\dfrac{CB}{CA}=\dfrac{12}{9}=\dfrac{4}{3}\)
\(\cot\widehat{B}=\dfrac{CB}{CA}=\dfrac{12}{9}=\dfrac{4}{3}\)

ta có:
. \(\hept{\begin{cases}tan\alpha=\frac{sin\alpha}{cos\alpha}\\cot\alpha=\frac{cos\alpha}{sin\alpha}\\tan\alpha\times cot\alpha=1\end{cases}}\)

Hướng dẫn:
∆
ABC ∼
∆
HBA nên 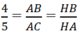
Suy ra HB = 4/5HA = 48/5 = 9,6. Chọn B.
D.sin C =3/5 nhá xin like với;)
Chọn D