Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Dựa vào giản đồ xét tam giác vuông OAB có
\(\sin60=\frac{Uc}{U_{ }AB}\Rightarrow U_C=100.\sin60=50\sqrt{3}V\Rightarrow Z_C=\frac{U_C}{I}=\frac{50\sqrt{3}}{0.5}=100\sqrt{3}\Omega\)
=> \(C=\frac{1}{Z_C.\omega}\)
\(\cos60=\frac{U_R}{U_{AB}}\Rightarrow U_R=50\Omega\Rightarrow R=\frac{U_R}{I}=100\Omega\)
2. Công suất trên mạch có biểu thức
\(P=I^2R=\frac{U^2}{R^2+\left(Z_L-Z_C\right)^2}.R\\=\frac{U^2}{R^{ }+\frac{\left(Z_L-Z_C\right)^2}{R}}\)
L thay đổi để P max <=> Mẫu Min => áp dụng bất đẳng thức cô-si cho hai số không âm=> \(R=\left|Z_L-Z_C\right|\)
=> \(R=100-40=60\Omega\)
=>

Bài 1:
Để công suát tiêu thụ trê mạch cực đại thì:
\((R+r)^2=(R_1+r)(R_1+r)\)
\(\Rightarrow (R+10)^2=(15+10)(39+10)\)
\(\Rightarrow R=25\Omega\)
Bài 2: Có hình vẽ không bạn? Vôn kế đo hiệu điện thế của gì vậy?

\(Z_L=\omega L=100\Omega\)
Ta áp dụng một tính chất của mạch RLC khi C thay đổi để Uc max là lúc đó u mạch vuông pha với uRL.
Như vậy, bài này theo giả thiết uAB lệch pha pi/2 so với uAM là thỏa mãn điều kiện trên.
=> \(Z_C=\frac{R^2+Z_L^2}{Z_L}=\frac{50^2+100^2}{100}=125\Omega\)
=> C

Đáp án C
+ Khi mắc vào hai cực ND một điện áp không đổi → có dòng trong mạch với cường độ I = 1,5 A
→ ND không thể chứa tụ (tụ không cho dòng không đổi đi qua) và
![]()
+ Mắc vào hai đầu đoạn mạch MB một điện áp xoay chiều thì uND sớm pha hơn uMN một góc 0,5π → X chứa điện trở RX và tụ điện C, Y chứa cuộn dây L và điện trở RY.
→ với V1 = V2 → UX = UY = 60 V → ZX = ZY = 60 Ω.
+ Cảm kháng của cuộn dây Ω
.![]()
+ Với uMN sớm pha 0,5π so với uND và →
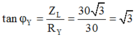
φY = 600 → φX = 300.
→ 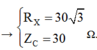
+ Điện áp hiệu dụng hai đầu MN:
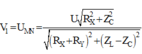
.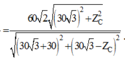
+ Sử dụng bảng tính Mode → 7 trên Caio ta tìm được V1max có giá trị lân cận 105 V.

\(U_{RC}=const=U\) khi \(Z_{L1}=2Z_C=R\)
Mặt khác L thay đổi để : \(U_{Lmax}:U_{Lmax}=\frac{U\sqrt{R^2+Z^2_C}}{R}=\frac{U\sqrt{2^2+1}}{2}=\frac{U\sqrt{5}}{2}\)
\(\Rightarrow chọn.D\)
+,có C=C1=>U_R=\frac{U.R}{\sqrt{R^2+(Zl-ZC1)^2}}
+,U R ko đổi =>Zl=ZC1
+,có c=C1/2=>ZC=2ZC1
=>U(AN)=U(RL)=\frac{U\sqrt{r^2+Z^2l}}{\sqrt{R^2+(Zl-2Z^2C1)}}=u=200V

Áp dụng công thức:
$P_1=\dfrac{U^2}{R_1}\cos ^2\varphi _1$ và $P_2=\dfrac{U^2}{R_2}\cos ^2\varphi _2$
$\Leftrightarrow 60=\dfrac{100^2}{50}\cos ^2\varphi _1\Leftrightarrow \cos ^2\varphi _1=\dfrac{3}{10}$
$\Leftrightarrow \cos ^2\varphi _2=\dfrac{9}{20}$
$\Leftrightarrow P_2=180$
$\dfrac{P_2}{P_1}=3$

Đáp án A
+ Khi mắc vào hai cực ND một điện áp không đổi => có dòng trong mạch với cường độ I = 1,5 A => ND không thể chứa tụ (tụ không cho dòng không đổi đi qua) và R Y = 40 1 , 5 = 30
+ Mắc vào hai đầu đoạn mạch MB một điện áp xoay chiều thì u N D sớm pha hơn u M N một góc 0 , 5 π => X chứa điện trở và tụ điện C, Y chứa cuộn dây L và điện trở R Y .
=> với
![]()
+ Cảm kháng của cuộn dây
![]()
+ Với u M N sớm pha 0 , 5 π so với u N D và
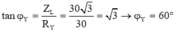
→ φ x = 30 0
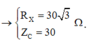
+ Điện áp hiệu dụng hai đầu MN:
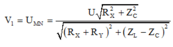
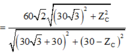
+ Sử dụng bảng tính Mode 7 trên Casio ta tìm được V 1 m a x có giá trị lân cận 90 V

Cách giải: Đáp án A
+ Khi mắc vào hai cực ND một điện áp không đổi => có dòng trong mạch với cường độ
![]()
không thể chứa tụ (tụ không cho dòng không đổi đi qua) và
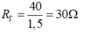
+ Mắc vào hai đầu đoạn mạch MB một điện áp xoay chiều thì u ND sớm pha hơn u MN một góc 5 X chứa điện trở R X và tụ điện C, Y chứa cuộn dây L và điện trở RY
=>với
![]()
+ Cảm kháng của cuộn dây
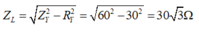
+ Với u MN sớm pha 0 , 5 π so với u ND và
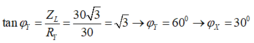
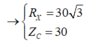
+ Điện áp hiệu dụng hai đầu MN:
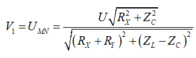
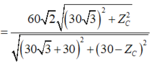
Sử dụng bảng tính Mode => 7 trên Casio ta tìm được V 1 max có giá trị lân cận 90V

Giả thiết bài toán ta thấy cuộn dây phải có điện trở r.
Bài này vẽ giản đồ véc tơ chung gốc, tính được uMB sớm pha với i 600, uAN trễ pha với i là 600.
Từ đó suy ra \(U_{LC}=120V\), \(U_C=240V\)
--> \(U_L=360V\)
--> \(Z_L=120\sqrt{3}\Omega\)
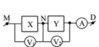
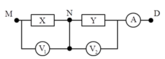
105*