Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A.
(h.2.59) Trong tam giác ABC vuông tại A, ta có:
AC = BC.sin30 ° = a;
AB = BC.cos30 ° = a 3 .
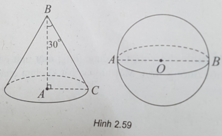
Diện tích toàn phần hình nón là:
S 1 = S xq + S đáy = πRl + πR 2 = πa . 2 a + πa 2 = 3 πa 2
Diện mặt cầu đường kính AB là:
S 2 = πAB 2 = π a 3 2 = 3 πa 2
Từ đó suy ra, tỉ số S 1 / S 2 = 1

Chọn D.
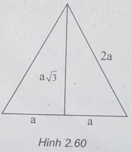
(h.2.60) Bán kính đáy của hình nón là a, đường sinh của hình nón là 2a.
Do đó, ta có:
S 1 = π Rl = π .a.2a = 2 πa 2 (1)
Mặt cầu có bán kính là a 3 /2, nên ta có:
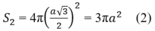
Từ (1) và (2) suy ra: 2 S 2 = 3 S 1

\(\dfrac{1}{2}l^2=2a^2\Rightarrow l=2a\)
\(2R=\sqrt{2}l\Rightarrow R=\dfrac{l}{\sqrt{2}}=a\sqrt{2}\)
\(h=\sqrt{l^2-R^2}=a\sqrt{2}\)
\(\Rightarrow V=\dfrac{1}{3}\pi R^2.h=\dfrac{2\sqrt{2}\pi a^3}{3}\)



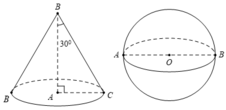





Lời giải:
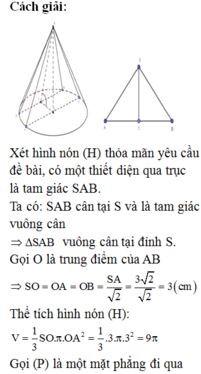
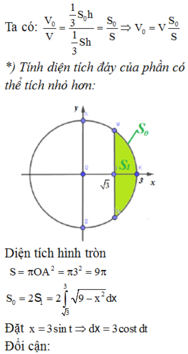
Gọi thiết diện qua trục là tam giác đều \(ABC\) có cạnh là $a$ , tâm đường tròn là \(H\)
Ta có \(BH=\frac{a}{2},AH=\frac{\sqrt{3}a}{2}\)
Theo hệ thức trong tam giác vuông \(\frac{1}{d(H,AB)^2}=\frac{1}{BH^2}+\frac{1}{AH^2}=\frac{1}{9}\)
\(\Leftrightarrow \frac{16}{3a^2}=\frac{1}{9}\Rightarrow a=4\sqrt{3}\)
Suy ra diện tích toàn phần của hình nón:
\(S_{tp}=\pi Rl+\pi R^2=36\pi\)