Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

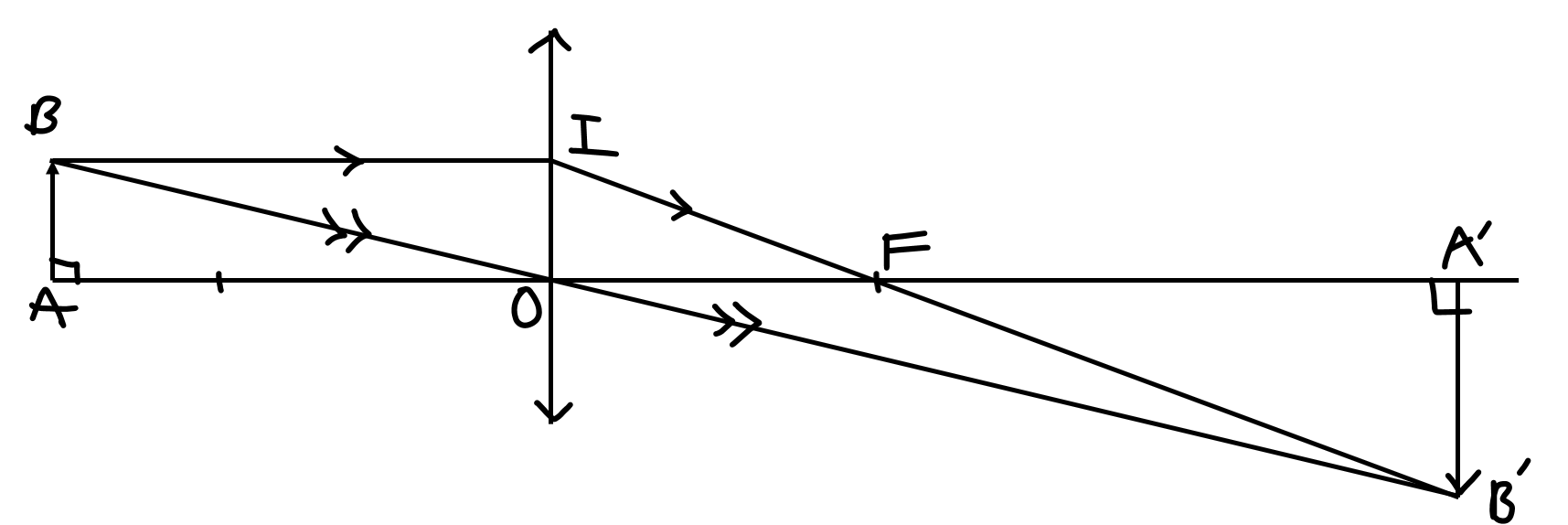
△OAB ∼ △OA'B' (g-g) \(=>\dfrac{OA}{OA'}=\dfrac{AB}{A'B'}=>\dfrac{d}{d'}=\dfrac{h}{h'}\left(1\right)\)
△FOI ∼ △FA'B' (g-g) \(=>\dfrac{OF}{FA'}=\dfrac{OI}{A'B'}\)
mà FA' = OA' - OF; OI = AB
\(=>\dfrac{OF}{OA'-OF}=\dfrac{AB}{A'B'}=>\dfrac{f}{d'-f}=\dfrac{h}{h'}\left(2\right)\)
từ (1)(2) \(=>\dfrac{d}{d'}=\dfrac{f}{d'-f}=>dd'-df=d'f\)
\(=>dd'-d'f=df=>d'\cdot\left(d-f\right)=df\\ =>d'=\dfrac{df}{d-f}=\dfrac{24\cdot16}{24-16}=48\left(cm\right)\left(3\right)\)
thay (3) vào (1) ta được: \(\dfrac{24}{48}=\dfrac{2}{h'}\)
\(=>h'=\dfrac{2\cdot48}{24}=4\left(cm\right)\)
vậy khoảng cách từ ảnh đến thấu kính là 48 cm; chiều cao ảnh là 4cm

Khoảng cách từ ảnh đến thấu kính là:
Áp dụng công thức tính thấu kính:
\(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\Rightarrow d'=\dfrac{d.f}{d-f}=\dfrac{8.4}{8-4}=8\left(cm\right)\)
Chiều cao của ảnh:
Ta có: \(\dfrac{d}{d'}=\dfrac{h}{h'}\Rightarrow h'=\dfrac{d'.h}{d}=\dfrac{8.2}{8}=2\left(cm\right)\)

Hướng dẫn:
Nhận xét:
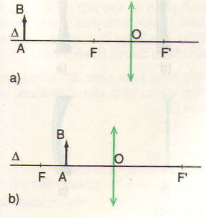
+ Vật AB cách thấu kính 36cm, ngoài khoảng tiêu cự, ảnh thật, ngược chiều vật
+ Khi vật AB cách thấu kính 8cm, trong khoảng tiêu cự, ảnh là ảo, cùng chiều vật và lớn hơn vật
Hướng dẫn:

Nhận xét:
+ Vật AB cách thấu kính 36cm, ngoài khoảng tiêu cự, ảnh thật, ngược chiều vật
+ Khi vật AB cách thấu kính 8cm, trong khoảng tiêu cự, ảnh là ảo, cùng chiều vật và lớn hơn vật
Hướng dẫn:

Nhận xét:
+ Vật AB cách thấu kính 36cm, ngoài khoảng tiêu cự, ảnh thật, ngược chiều vật
+ Khi vật AB cách thấu kính 8cm, trong khoảng tiêu cự, ảnh là ảo, cùng chiều vật và lớn hơn vật
Hướng dẫn:
Đặt một thấu kính hội tụ sát vào một trang sách, khi ấy các dòng chữ (coi là vật) sẽ nằm trong khoảng tiêu cự của thấu kính, cho hình ảnh các dòng chữ (là ảnh) sẽ cùng chiều và lớn hơn vật, do đó sẽ dễ đọc hơn. Từ từ dịch chuyển thấu kính ra xa, ảnh càng to và càng dễ đọc.
Tuy nhiên, khi dịch chuyển đến một vị trí nào đó, ta lại nhìn thấy ảnh của dòng chữ ngược chiều với vật. Đó là ảnh thật của dòng chữ tạo bởi thấu kính hội tụ. Vị trí đó trùng với tiêu điểm của thấu kính hội tụ, nên khi tiếp tục dịch chuyển ra xa thì dòng chữ (vật) nằm ngoài khoảng tiêu cự, cho ta ảnh ngược chiều, khó đọc

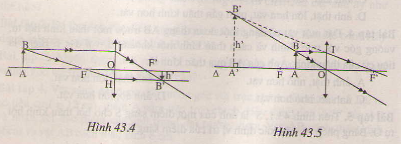
a) dựng ảnh A'B' của AB qua thấu kính hội tụ
sử dung 2 trong 3 tia sáng đặc biêt
tia (1) : từ A kẻ đường thẳng đi qua quang tâm O cho tia sáng truyền thẳng
tia (2): từ A kẻ đường thẳng song song với trục chính của thấu kính cho tia sáng đi qua tiêu điểm ảnh (F') của thấu kính
giao của 2 tia tại A'
từ A' kẻ đường thẳng vuông góc với trục chính tại B'
b) ΔOAB∞ΔOA′B′(g.g)⇒OA/OA'=AB/A′B′⇔d/d′=AB/A′B′(1)
mà:
ΔOIF′∞ΔA′B′F′(g.g)⇒OI/A′B′=OF′/F′A′⇔AB/A′B′=f/d′−f(2)
từ (1) và (2) ta có:
d/d′=f/d′−f⇔24/d′=12/d′−12⇒d′=24cm
độ cao của ảnh:
A′B/′AB=d′/d⇒A′/B′=2.24/24=2cm

Chúc bn học tốt

a. Dựng ảnh A'B'

b) d > f , ảnh lớn hơn và ngược chiều với vật
c)
Tóm tắt:
OF = 12cm
OA = 18cm
AB = 6cm
A'B' = ?
Giải:
Δ ABF ~ OIF
\(\Rightarrow\dfrac{AB}{OI}=\dfrac{AF}{OF}\Leftrightarrow\dfrac{AB}{A'B'}=\dfrac{OA-OF}{OF}\Leftrightarrow\dfrac{6}{A'B'}=\dfrac{18-12}{12}\)
=> A'B' = 12cm

AB = 2cm
OA = 15cm
OF = 10cm
a. Hình vẽ tham khảo ảnh
b. Ta có 1/A'O = 1/OF - 1/AO = 1/10 - 1/15 = 1/30 hay A'O = 30cm
Vì A'B'/AB = A'O/AO nên A'B' = (AB.A'O)/AO = (2.30)/15 = 4cm
Vậy ảnh cao 4cm và cách thấu kính một đoạn 30cm
(Cách chứng minh như trong hình vẽ)