Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Ta có λ = v f = 1 50 = 0 , 02 ( m ) = 2 c m
Hai điểm gần nhất dao động ngược pha cách nhau λ 2 = 1 c m

Đáp án D
Hai điểm M, N dao động với biên độ cực đại, thuộc đường nối AB sẽ dao động cùng pha hoặc ngược pha.
Khi M có tốc độ cực đại thì N có tốc độ cụ đại (vì cùng đi qua vị trí cân bằng) → T/2 → N lại có tốc độ cực đại.

Khi hệ vân giao thoa đã ổn định thì trung điểm I của S 1 S 2 lại luôn luôn là cực đại giao thoa. Do đó, ta phải có :
S 1 I = S 2 I = k λ /2 + λ /4 = (2k + 1) λ /4
S 1 S 2 = 2 S 1 I = (2k + 1) λ /2
Ban đầu ta đã có : S 1 S 2 = 8cm = 10 λ = 20 λ /2
Vậy chỉ cần tăng khoảng cách S 1 , S 2 thêm λ /2 tức là 0,4 cm.
Khi đó nếu không kể đường trung trực của S 1 S 2 thì có 20 gợn sóng hình hypebol (vì gợn sóng là quỹ tích những điểm dao động mạnh hơn cả).

Chọn đáp án B
Đặt A B = l = 50 c m , bước sóng λ = v . T = 8 c m .
Khi hai nguồn dao động cùng pha,số vân có biên độ dao động cực đại bằng số giá trị của k thoả mãn
− l λ < k < l λ ⇒ − 6,25 < k < 6,25 ⇒ k = 0, ± 1,...., ± 6.
→ Có 13 vân cực đại, vân chính giữa là vân cực đại bậc k = 0, vân cực đại gần B nhất là vân bậc 6. Điểm M trên đường Bx vuông góc với AB sóng có biên độ cực đại và M gần B nhất thì M là giao điểm của Bx và vân cực đại bậc 6, MA – MB = k.λ= 6.8 = 48 cm.
⇒MA = MB + 48 (cm). MB⊥AB
⇒ M A 2 = A B 2 + M B 2 ⇔ ( M B + 48 ) 2 = A B 2 + M B 2 ⇔ M B 2 + 96 M B + 48 2 = 50 2 + M B 2 ⇔ M B = 50 2 − 48 2 96 = 2,04 c m

Đáp án B
Đặt AB =l = 50 cm, bước sóng λ = v.T = 8cm.
Khi hai nguồn dao động cùng pha,số vân có biên độ dao động cực đại bằng số giá trị của k thoả mãn
- 1 λ < k < 1 λ ⇒ - 6 , 25 < k < 6 , 25 ⇒ k = 0 , ± 1 , . . . , ± 6
→ Có 13 vân cực đại, vân chính giữa là vân cực đại bậc k = 0, vân cực đại gần B nhất là vân bậc 6. Điểm M trên đường Bx vuông góc với AB sóng có biên độ cực đại và M gần B nhất thì M là giao điểm của Bx và vân cực đại bậc 6, MA – MB = k.λ= 6.8 = 48 cm.
⇒ MA = MB + 48 (cm). MB⊥AB
⇒ MA 2 = AB 2 + MB 2 ⇔ ( MB + 48 ) 2 = AB 2 + MB 2 ⇔ MB 2 + 96 MB + 48 2 = 50 2 + MB 2 ⇔ MB = 50 2 - 48 2 96 = 2 , 04 cm

Mình ra có 4 điểm thôi bạn ơi, xem hộ mình xem có nhầm lẫn ở đâu không nhé (mình tin là các bước làm là đúng rồi, sợ thay sai ở đâu đó thôi)
Gọi giao điểm của đường tròn với đoạn AB ll là D, E (bạn vẽ hình ra cho dễ nhìn nhé). để xác định số điểm theo đề ta chỉ cần xác định số điểm M nằm trên đoạn DE dao động với biên độ 8cm
Ta có: \(U_{am}=3cos\left(10\pi t-\frac{10\pi d_1}{50}\right)\)(d1:khoảng cách MA)
\(U_{bm}=5cos\left(10\pi t-\frac{10\pi\left(30-d_1\right)}{50}+\frac{\pi}{3}\right)=5cos\left(10\pi t+\frac{\pi}{5}d_1+\frac{\pi}{3}\right)\)
độ lệch pha giữa hai dao động thành phần: \(\Delta\varphi=\frac{2\pi}{5}d_1+\frac{\pi}{3}\left(1\right)\)
ta có biên độ dao động tại M (theo tổng hợp dao dộng, bạn vẽ giản đồ vectơ cho dễ nhìn): (một cách trực quan ta thấy luôn 8=3+5. do đó hai dao động thành phần phải cùng pha. tuy nhiên để ở đây mình làm theo công thức đơn thuần) \(8^2=5^2+3^2+2.5.3.cos\Delta\varphi\Rightarrow\Delta\varphi=2k\pi\left(2\right)\)
từ (1) và (2) và M thuộc DE ta được \(13\le d_1=5k-\frac{5}{6}\le23\Rightarrow3\le k\le4\)
=>có 2giá trị của k tương ứng với có 2 điểm M nằm trên đoạn DE không trùng với D, E dao động với biên độ 8cm (nói cách khác là thuộc khoảng DE) =>trên đường tròn đề bài ra có 2*2=4 điểm

Ta có : λ = v/f = 80/100 = 0,8cm và d 1 = d 2 = d = 8cm.
Theo Bài 8 (SGK Vật lí 12), ta có :
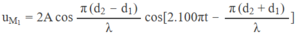
d 1 + d 2 = 16cm = 20 λ d 2 - d 1 = 0
ta được : u M 1 = 2Acos(200 π t - 20 π )