Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Sử dụng tính đơn điệu của hàm số, đánh giá số nghiệm của phương trình.
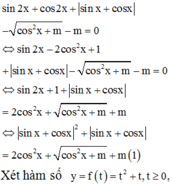
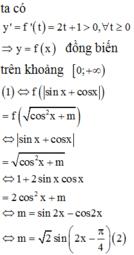

Vậy, có 3 giá trị nguyên của m thỏa mãn yêu cầu đề bài.

1.
\(3cos2x-7=2m\)
\(\Leftrightarrow cos2x=\dfrac{2m-7}{3}\)
Phương trình đã cho có nghiệm khi:
\(-1\le\dfrac{2m-7}{3}\le1\)
\(\Leftrightarrow2\le m\le5\)
2.
\(2cos^2x-\sqrt{3}cosx=0\)
\(\Leftrightarrow cosx\left(2cosx-\sqrt{3}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=0\\cosx=\dfrac{\sqrt{3}}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{2}+k\pi\\x=\pm\dfrac{\pi}{6}+k2\pi\end{matrix}\right.\)
\(\Rightarrow\) Có 4 nghiệm \(\dfrac{\pi}{2};\dfrac{3\pi}{2};\dfrac{\pi}{6};\dfrac{11\pi}{6}\) thuộc đoạn \(\left[0;2\pi\right]\)

Đáp án B
PT

Đặt
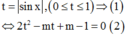
Để (1) có nghiệm thì (2) có nghiệm ![]() có nghiệm
có nghiệm ![]()
Suy ra 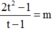 có nghiệm
có nghiệm ![]()
Xét hàm số 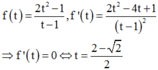
Lập bảng biến thiên hàm số 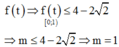

Chọn đáp án D
Phương pháp
Cho ba số a, b, c lập thành CSN thì ta có: b 2 = a c .
Cách giải
Ta có: ( x - 1 ) ( x - 3 ) ( x - m ) = 0
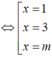
Phương trình đã cho có 3 nghiệm phân biệt
![]()
+) Giả sử 1; 3; m lập thành 1 CSN tăng
![]()
+) Giả sử m; 1; 3 lập thành 1 CSN tăng
![]()
+) Giả sử 1; m; 3 lập thành 1 CSN tăng
![]()
Vậy có 3 giá trị m thỏa mãn
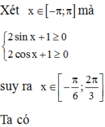
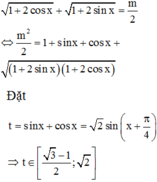
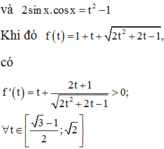
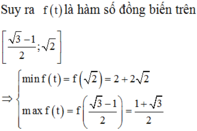
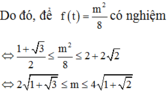
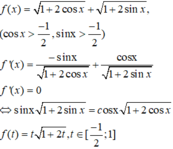
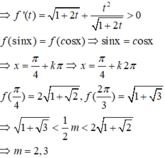



Câu 1:
\(2\sin x-\sqrt{3}=0\\ \Leftrightarrow\sin x=\dfrac{\sqrt{3}}{2}=\sin\dfrac{\pi}{3}\\ \Leftrightarrow\left[{}\begin{matrix}x_1=\dfrac{\pi}{3}+k_12\pi\\x_2=\pi-\dfrac{\pi}{3}+k_22\pi=\dfrac{2\pi}{3}+k_22\pi\end{matrix}\right.\left(k_1,k_2\inℤ\right)\)
Mà: \(x\in\left[0;2\pi\right]\) do đó nên: \(k_1=0,k_2=0\)
Vậy tập nghiệm pt là: \(S=\left\{\dfrac{\pi}{3};\dfrac{2\pi}{3}\right\}\) (2 nghiệm => D)
Câu 2:
Vì: \(-1\le\cos x\le1\forall x\)
\(\Rightarrow-1\le m+1\le1\\ \Leftrightarrow-2\le m\le0\)
Mà: \(m\inℤ\Rightarrow m\in\left\{-2;-1;0\right\}\) (C)
Câu 1: \(2\cdot sinx-\sqrt{3}=0\)
=>\(sinx=\dfrac{\sqrt{3}}{2}\)
=>\(\left[{}\begin{matrix}x=\dfrac{\Omega}{3}+k2\Omega\\x=\Omega-\dfrac{\Omega}{3}+k2\Omega=\dfrac{2}{3}\Omega+k2\Omega\end{matrix}\right.\)
Để \(x\in\left[0;2\Omega\right]\) thì \(\left[{}\begin{matrix}\dfrac{\Omega}{3}+k2\Omega\in\left[0;2\Omega\right]\\\dfrac{2}{3}\Omega+k2\Omega\in\left[0;2\Omega\right]\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2k+\dfrac{1}{3}\in\left[0;2\right]\\2k+\dfrac{2}{3}\in\left[0;2\right]\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}2k\in\left[-\dfrac{1}{3};\dfrac{5}{3}\right]\\2k\in\left[-\dfrac{2}{3};\dfrac{4}{3}\right]\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}k\in\left[-\dfrac{1}{6};\dfrac{5}{6}\right]\\k\in\left[-\dfrac{1}{3};\dfrac{2}{3}\right]\end{matrix}\right.\Leftrightarrow k=0\)
=>Chọn B
Câu 2:
Để phương trình cosx =m+1 có nghiệm thì -1<=m+1<=1
=>-2<=m<=0
mà m nguyên
nên \(m\in\left\{-2;-1;0\right\}\)
=>Chọn C