Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

gọi vận tốc xe khách là x (km/h) (x>0)
vận tốc xe du lịch là x+20(km/h)
thời gian xe khách đi từ A đến khi gặp nhau là \(\frac{100}{x}\)(h)
thời gian xe du lịch đi từ B đến khi gặp nhau là \(\frac{100}{x+20}\)(h)
theo bài ra ta có phương trình: \(\frac{100}{x}\)= \(\frac{100}{x+20}\)+\(\frac{5}{6}\)
=> 600x+12000=600x + \(5x^2\)+100x
=> \(\hept{\begin{cases}x=40\left(tm\right)\\x=-60\left(L\right)\end{cases}}\)
Vậy vạn tốc xe khách là 40km/h
xe du lịch là 60km/h
Có chỗ mk lm ra kết quả luôn , hơi tắt 1 tí mog bn giải nốt

Ta có: 4 giờ 20 phút= 13/3 giờ
Gọi độ dài quãng đường AC là x(km)
Gọi độ dài quãng đường CB là y(km)
Điều kiện x > 0 và y > 20
Lúc đó thời gian người đi xe máy đi trên quãng đường AC là x/30 (giờ)
Thời gian người đi xe máy đi trên quãng đường CB là y/20 (giờ)
Theo đề bài, thời gian cả thảy đi từ A đến B là 4 giờ 20 phút nên ta có phương trình:
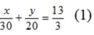
Vì quãng đường AB ngắn hơn quãng đường BC là 20 km nên ta có phương trình: y – x = 20 (2)
Từ (1) và (2) ta có hệ phương trình:


Vậy quãng đường AC dài 40km, quãng đường CB dài 60km.

Gọi \(x,y\) là vận tốc của xe khách và xe du lịch \(\left(x,y>0\right)\left(km/h\right)\)
\(36p=0,6h\)
Theo đề bài, ta có hệ pt :
\(\left\{{}\begin{matrix}x+13=y\\\dfrac{156}{x}-\dfrac{156}{y}=0,6\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-y=-13\\-156x+156y=0,6\end{matrix}\right.\)
\(\)Bai có đúng số không ấy, chứ mình ra vô nghiệm \(;-;\)

Gọi x ( km/h) là vận tốc xe du lịch (x>0)
=> x-20 (km/h) là vận tốc xe khách.
Thời gian xe du lịch đi hết quãng đường AB là: \(\frac{100}{x}\) (giờ).
Thời gian xe khách đi hết quãng đường AB là: \(\frac{100}{x-20}\)(giờ).
Theo đề bài, ta có phương trình:
\(\frac{100}{x-20}-\frac{100}{x}=\frac{5}{6}\)
<=> \(x=60\) (nhận)
Trả lời: Vận tốc xe du lịch là 60 (km/h).
Vận tốc xe khách là 40 (km/h).

Lời giải:
Đổi 4h30 = $4,5$ h
Vận tốc trên quãng đường CB là $a$ km/h thì vận tốc trên $AC$ là $a+20$ (km/h)
Quãng đường $AC=BC+10$ (km)
Tổng thời gian đi quãng đường AB: $\frac{AC}{v_{AC}}+\frac{CB}{v_{CB}}=4,5$
$\Leftrightarrow \frac{BC+10}{a+20}+\frac{BC}{a}=4,5$
Khai thác được đến đây thì không biết bạn muốn tìm cái gì?