Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi cạnh đáy của tam giác ban đầu là \(x\left(dm,x>0\right)\)
Vì tam giác ban đầu có chiều cao bằng \(\frac{3}{4}\)cạnh đáy nên chiều cao của tam giác ban đầu là \(\frac{3}{4}x\)
Diện tích của tam giác ban đầu là \(\frac{1}{2}.x.\frac{3}{4}x=\frac{3}{8}x^2\left(dm^2\right)\)
Vì chiều cao tăng thêm 3dm nên chiều cao của tam giác lúc sau là \(\frac{3}{4}x+3\left(dm\right)\)
Cạnh đáy giảm 2dm nên cạnh đáy của tam giác lúc sau là \(x-2\left(dm\right)\)
Diện tích của tam giác lúc sau là \(\frac{1}{2}\left(\frac{3}{4}x+3\right)\left(x-2\right)\left(dm^2\right)\)
Vì diện tích của tam giác lúc sau lớn hơn diện tích tam giác ban đầu là \(12dm^2\)nên ta có phương trình:
\(\frac{1}{2}\left(\frac{3}{4}x+3\right)\left(x-2\right)-\frac{3}{8}x^2=12\)\(\Leftrightarrow\left(\frac{3}{8}x+\frac{3}{2}\right)\left(x-2\right)-\frac{3}{8}x^2=12\)\(\Leftrightarrow\frac{3}{8}x^2-\frac{3}{4}x+\frac{3}{2}x-3-\frac{3}{8}x^2=12\)\(\Leftrightarrow\frac{3}{4}x=15\Leftrightarrow x=20\)(nhận)
Vậy chiều cao của tam giác ban đầu là 15dm, cạnh đáy ban đầu là 20dm.

Gọi độ dài cạnh đáy là x (dm), x > 2
Suy ra, chiều cao tam giác là
3 4 x (dm)
Vậy diện tích tam giác là:
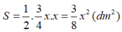
Chiều cao của tam giác khi tăng thêm 3dm là:
3 4 x + 3 (dm)
Cạnh đáy của tam giác khi giảm đi 2dm là: x – 2 (dm)
Vậy diện tích mới của tam giác là:
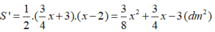
Theo đề bài ta có phương trình:
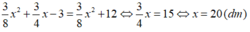
Vậy độ dài cạnh đáy là 20 dm, chiều cao là 3 4 .20 = 15 dm

Gọi chiều cao của tam giác là h, cạnh đáy tam giác là a. (h, a ∈ ℕ * , dm); (a > 2)
Diện tích tam giác ban đầu là ah ( d m 2 )
Vì chiều cao bằng 1 4 cạnh đáy nên ta có phương trình h = 1 4 a
Nếu chiều cao tăng thêm 2 dm và cạnh đáy giảm đi 2 dm thì diện tích của nó tăng thêm 2,5 d m 2 .
Nên ta có phương trình 1 2 h + 2 a − 2 − 1 2 a h = 2 , 5
Ta có hệ phương trình:
h = 1 4 a 1 2 h + 2 a − 2 − 1 2 a h = 2 , 5 ⇔ h = 1 4 a − 2 h + 2 a − 4 = 5 ⇔ h = 1 4 a − 2. 1 4 a + 2 a = 9 ⇔ a = 6 h = 1 , 5 ( t m )
Vậy chiều cao và cạnh đáy của tấm bìa lần lượt là 1,5 dm và 6 dm
Đáp án: A

Gọi chiều dài và chiều rộng của khu vương hình chữ nhật lần lượt là x, y
(24 > x > y > 0; m)
Vì khu vườn hình chữ nhật có chu vi bằng 48 m nên ta có (x + y). 2 = 48
Nếu tăng chiều rộng lên bốn lần và chiều dài lên ba lần thì chu vi của khu vườn sẽ là 162m
Nên ta có phương trình (4y + 3x). 2 = 162
Suy ra hệ phương trình
x + y .2 = 48 4 y + 3 x .2 = 162 ⇔ x + 24 3 x + 4 y = 81 ⇔ x = 15 y = 9 (thỏa mãn)
Vậy diện tích khu vườn ban đầu là 15.9 = 135 m 2
Đáp án: C

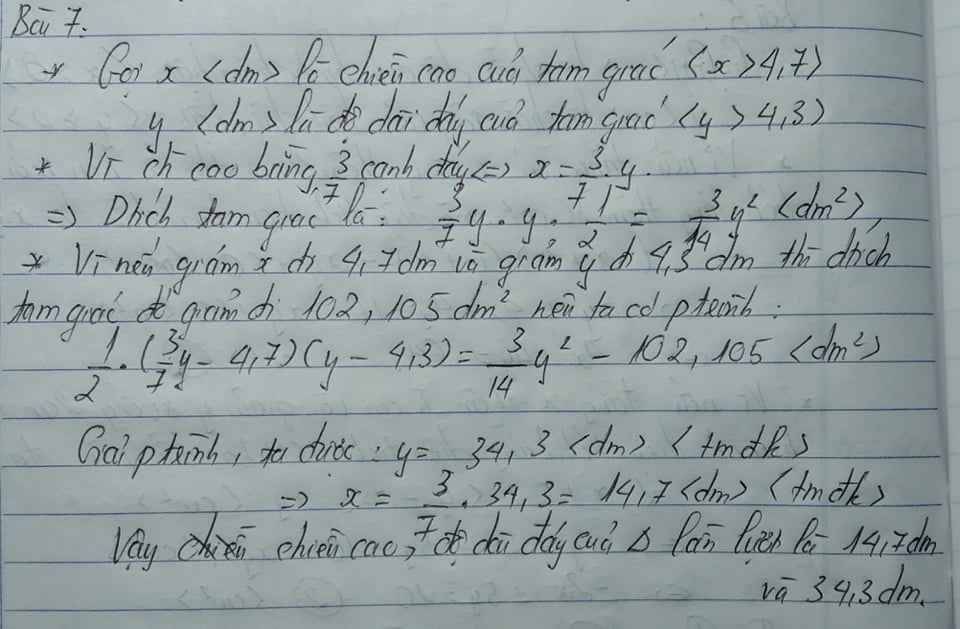
Câu 2:
Gọi a(m) và b(m) lần lượt là chiều dài và chiều rộng của khu vườn(Điều kiện: \(\left\{{}\begin{matrix}a>0\\b>0\\a\ge b\end{matrix}\right.\))
Vì chu vi của khu vườn là 48m nên ta có phương trình:
2(a+b)=48
hay a+b=24(1)
Vì khi tăng chiều rộng lên 4 lần và chiều dài lên 3 lần thì chu vi của khu vườn là 162m nên ta có phương trình:
\(2\cdot\left(3a+4b\right)=162\)
\(\Leftrightarrow3a+4b=81\)(2)
Từ (1) và (2) ta lập được hệ phương trình:
\(\left\{{}\begin{matrix}a+b=24\\3a+4b=81\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3a+3b=72\\3a+4b=81\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-b=-9\\a+b=24\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=9\left(nhận\right)\\a=24-9=15\left(nhận\right)\end{matrix}\right.\)
Diện tích ban đầu của khu vườn là:
\(S=ab=9\cdot15=135\left(m^2\right)\)