Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

+ - A B C q1 q2 E1 E2 E
Nhận xét: Do \(AB^2=AC^2+BC^2\) nên tam giác ABC vuông tại C.
Điện trường tổng hợp tại C là: \(\vec{E}=\vec{E_1}+\vec{E_2}\)
Suy ra độ lớn: \(E=\sqrt{E_1^2+E_2^2}\) (*) (do \(\vec{E_1}\) vuông góc với \(\vec{E_2}\) )
\(E_1=9.10^9.\dfrac{16.10^{-8}}{0,04^2}=9.10^5(V/m)\)
\(E_1=9.10^9.\dfrac{9.10^{-8}}{0,03^2}=9.10^5(V/m)\)
Thay vào (*) ta được \(E=9\sqrt2.10^5(V/m)\)

Bài làm.
Điện tích điểm q1 = 3.10-8 C đặt tại điểm A, q2 = - 4.10-8 C đặt tại điểm B, AB = 10cm.
Gọi C là điểmmà tại đó cường độ điện trường bằng không.
Gọi −−→E1CE1C→ và −−→E2CE2C→ là cường độ điện trường của q1 và q2 tại C.
Tại đó −−→E1CE1C→ = - −−→E2CE2C→. Hai vectơ này phải cùng phương, tức là điểm C phải nằm trên đường thẳng AB (Hình 3.3).
Hai vectơ này phải ngược chiều, tức là phải nằm ngoài đoan AB. Vì hai vectơ này phải có môđun bằng nhau, tức là điểm C gần A hơn B vì |q1| < |q2|.
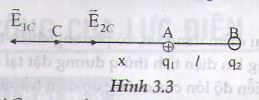
Đặt AN = l, AC = x, ta có :
k.|q1|ε.x2=k.|q2|ε.(l+x)2k.|q1|ε.x2=k.|q2|ε.(l+x)2 hay (l+xx)2=∣∣q2q1∣∣=43(l+xx)2=|q2q1|=43 hay x = 64,6cm.
Ngoài ra còn phải kể tất cả các điểm nằm rất xa q1 và q2. Tại điểm C và các điểm này thì cường độ điện trường bằng không, tức là không có điện trường

a.Vì q1 > 0 mà chúng đẩy nhau nên q2 > 0
F= \(\frac{k.\left|q_1q_2\right|}{r^2}\)
\(\Rightarrow\left|q_2\right|=\frac{F.r^2}{\left|q_1\right|}=\frac{6,75.10^{-5}.0,02^2}{\left|4.10^{-8}\right|}=0,675\left(C\right)\)
=>q2 =0,675 C
b)
b) \(E_{q_1}=\frac{k.\left|q_1\right|}{BH^2}=\frac{9.10^9.\left|4.10^{-8}\right|}{0,01^2}=3,6.10^6\frac{V}{m}\)
\(E_{q_2}=\frac{k.\left|q_2\right|}{AH^2}=\frac{9.10^9.\left|0,675\right|}{0,01^2}=6,075.10^{13}\frac{V}{m}\)
Vì vecto E1 ↑↑ vecto E2=>E=|E1-E2|=6,075.1013 V/m
\(E_{q_3}=\frac{k.\left|q_3\right|}{AH^2}=\frac{9.10^9.\left|-2.10^{-8}\right|}{\left(0,02.\sin45^o\right)^2}=621,5.10^3\frac{V}{m}\)
Vì vecto E vuông góc với Eq3 nên:
EH =\(\sqrt{E_{q_3}^2+E^2}=6,075.10^{13}\left(\frac{V}{m}\right)\)